SLED: Self Logits Evolution Decoding Boosts Factuality Without Retraining

Large language models deliver impressive results across many tasks, yet they still produce incorrect or ungrounded statements, often called hallucinations. A growing body of work explores how to reduce these errors not only through training-time fixes but also at inference time by adjusting how tokens are selected. 

A recent paper introduces Self Logits Evolution Decoding, or SLED, a decoding method that improves factuality by contrasting what the model's final layer is about to say with what earlier layers implicitly know and then nudging the output distribution accordingly.

Unlike retrieval-augmented methods that query external knowledge bases or techniques that require fine-tuning, SLED runs as a drop-in decoding strategy. It is designed to work across model families and sizes, including mixture of experts architectures, and the authors report consistent gains on factuality benchmarks such as TruthfulQA and FACTOR . The project page collects a complete picture of figures, tables, and links to code on the Project Website.

Key Takeaways

• Self Logits Evolution Decoding contrasts final-layer logits with early-layer logits, then updates the final logits with a single gradient-like step toward a latent target distribution derived from the model itself.
  
  
• It improves factuality on multiple-choice and long-paragraph evaluations, including TruthfulQA and FACTOR, over greedy decoding and DoLa, across Gemma-3 models from 1B to 27B parameters, with reported improvements also on Mixtral, Qwen, and gpt-oss models.
  
  
• No external retrieval or additional fine-tuning is required, and measured latency overhead is negligible in the reported experiments.
  
  
• Layer-wise signals are aggregated rather than relying on a single "premature" layer, addressing instability observed when selecting a single early layer in prior methods like DoLa (Chuang et al., 2024).
  
  
• SLED is compatible with other inference-time strategies, such as Contrastive Decoding and Inference-Time Intervention, yielding additional gains when combined (Li et al., 2022), (Li et al., 2023).
  
  
• Code is available: (JayZhang42/SLED) | Project page: (SLED).

How SLED Works

SLED starts from a simple idea that final-layer logits (the raw, unnormalized scores output by a LLM before applying the softmax function to produce probabilities) determine the next token distribution, but earlier layers often encode useful latent knowledge about what is true.

If we can estimate a directional signal from early layers that points toward the factual distribution, we can adjust the final logits before sampling. The method formalizes this as a one-step optimization of the final-layer distribution toward a latent target built from early-layer information.

Mathmatically we can define SLED by letting the model have N layers and vocabulary size d. For a given prefix, each layer n produces logits ${\ell }_{:,n}$ and probabilities $P_{{\text{logits}}_n}=\mathrm{softmax}({\ell }_{:,n}/\tau )$ where $\tau$ is temperature. The training objective can be seen as minimizing the divergence between the model distribution and a real-world target distribution $P_{\text{real}}$. 

At inference, $P_{\text{real}}$ is unknown, so SLED constructs an estimate $P_{\text{latent}}$ from early layers and then updates the final logits via a gradient-like step that reduces $\mathrm{KL}(P_{\text{latent}},P_{{\text{logits}}_N})$.

The update takes the form

$${\tilde{\ell }}_{i,N}={\ell }_{i,N}-\frac{\alpha }{\tau }(p_{i,N}-m_i),$$

where $p_{i,N}$ is the final-layer probability for token i, $m_i$ is the i-th component of the aggregated latent target $P_{\text{latent}}$, and $\alpha$ is the evolution rate that controls step size. This is analogous to a single gradient descent step on the final logits with respect to the KL divergence objective.

Constructing $P_{\text{latent}}$ is the core of SLED. For each early layer n, SLED compares the vector difference ${\ell }_{:,n}-{\ell }_{:,N}$ to the gradients one would obtain if the true next token were each vocabulary item i. Those per-token gradients, evaluated at layer n, have the form $(P_{{\text{logits}}_n}-e_i)/\tau$, where $e_i$ is the one-hot vector for token i. SLED scores tokens by cosine similarity between these gradients and ${\ell }_{:,n}-{\ell }_{:,N}$, clipping negatives to zero, then converts the scores into a soft distribution for that layer. Finally, it aggregates across layers with weights that emphasize layers whose signals align more consistently with the directional difference.

Two practical design choices keep SLED efficient and stable. First, it restricts computation to a small top-k set of tokens from the final layer, called the evolution scale k, and assigns a very low logit to others. Second, it squares per-token similarity scores when forming soft targets to slightly amplify differences without making them brittle. These choices, combined with a modest step size, avoid overcorrections and help preserve fluency.

Algorithm 1: Self Logits Evolution Decoding

1. Initialization: Let the LLM have $N$ layers. Given input tokens, evolution rate $\alpha$, evolution scale $k>0$, small constant $\eta \ll 0$, temperature $\tau$, and one-hot vectors $\{P_{e_i}\}$ 

2. Feed the inputs into the LLM to obtain the $logit{s}_n=({\ell }_{1,n},{\ell }_{2,n},...,{\ell }_{d,n})$

and probabilities

$P_{logit{s}_n}=(p_{1,n},p_{2,n},...,p_{d,n})=softmax(logit{s}_n/\tau )$

where $n\le N$

3. Identify top-$k$ tokens with highest logits in final layer $N$, denote indices as $I_k$

4. For each early layer n ($n<N$) do

  ​a. Compute difference for top-k logits: 

$$logit{s}_n-logit{s}_N$$

​b. Compute cosine similarity:

$$m_i^{(n)}={[max(CosSim({\text{logits}}_n-{\text{logits}}_N,P_{{\text{logits}}_n}-P_e),0)]}^2$$

where $i\in I_k$

5. Compute weighted average: 

$$m_i=\frac{\sum _{n=1}^N{m}_i^{(n)}}{\sum _{n=1}^N\sum _{j\in I_k}{m}_j^{(n)}}$$

across different layers for each  $i\in I_k$

5. For each token $i=1$ to $d$:

   - If $i\in I_k$: 

     $${\tilde{\ell }}_{i,N}={\ell }_{i,N}-\frac{\alpha }{\tau }(p_{i,N}-m_i)$$

   - Else:  $${\tilde{\ell }}_{i,N}=\eta$$

End For

6. Output the self evolved logits 

$${\widetilde{\text{login}}}_N=({\overrightarrow{\ell }}_{(1,N)},\dots ,{\overrightarrow{\ell }}_{(i,N)},\dots ,{\overrightarrow{\ell }}_{(d,N)})$$

Method Details And Practical Tips

Three knobs matter in practice. The evolution rate $\alpha$ sets the step size - too small and changes vanish, too large and outputs may overcorrect. The evolution scale k controls how many top tokens get explicitly updated - a small k keeps cost down and discourages spurious diversions. 

The temperature $\tau$ affects both the sharpness of probability distributions and the update magnitude, since the gradient terms scale with 1/tau. In the paper's experiments, modest settings work well and the method is stable across model sizes.

A concise pseudocode view of a single decoding step is shown above in Algorithm 1.

This design preserves two desirable properties: it biases toward directions supported by multiple layers and it calibrates the update against the model's own confidence. Both reduce the risk of enforcing a single-layer hunch that could be wrong.

Why It Matters

Inference-time methods are attractive because they can be deployed without retraining and can complement retrieval or alignment techniques. Prior approaches like DoLa contrast an early layer with the final layer and pick a single "premature" layer by a divergence criterion, but performance can degrade when the candidate set grows, indicating instability in selecting that single layer (Chuang et al., 2024). SLED counters this by aggregating signals across layers, building a soft latent target that acts as a regularized estimate of the true distribution.

The approach fits into a broader trend of leveraging models' internal knowledge at inference time. That includes contrastive decoding (Li et al., 2022), inference-time intervention (Li et al., 2023), and methods that combine retrieval with decoding (Lewis et al., 2020). SLED's optimization view offers a clear, interpretable handle to reason about why it improves factuality and how it trades off step size, layer weights, and top-k selection.

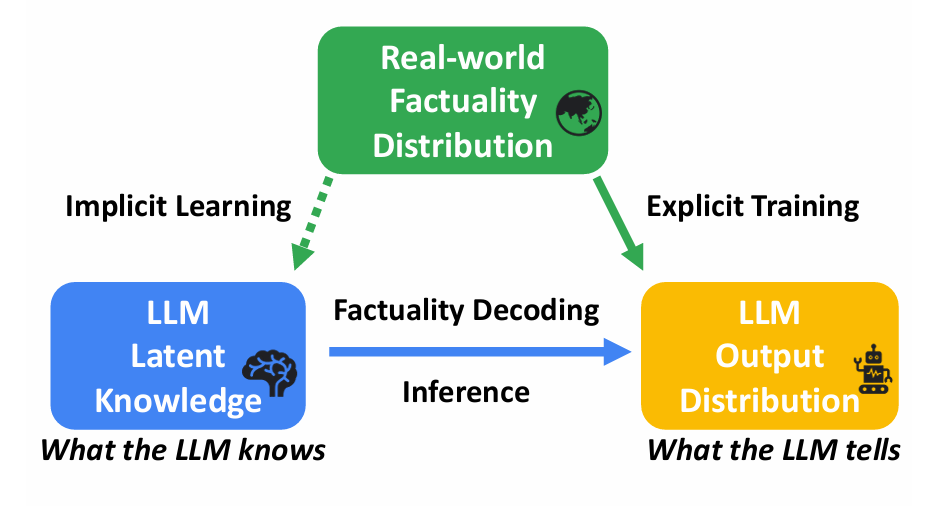
Figure 1: Factuality decoding overview.

Discussion: Results, Figures, And Evaluation

The paper evaluates SLED across Gemma-3 models from 1B to 27B parameters, both pretraining-aligned and instruction-tuned variants, and reports consistent gains on TruthfulQA's MC1 and MC3 metrics and on the long-paragraph FACTOR benchmark. 

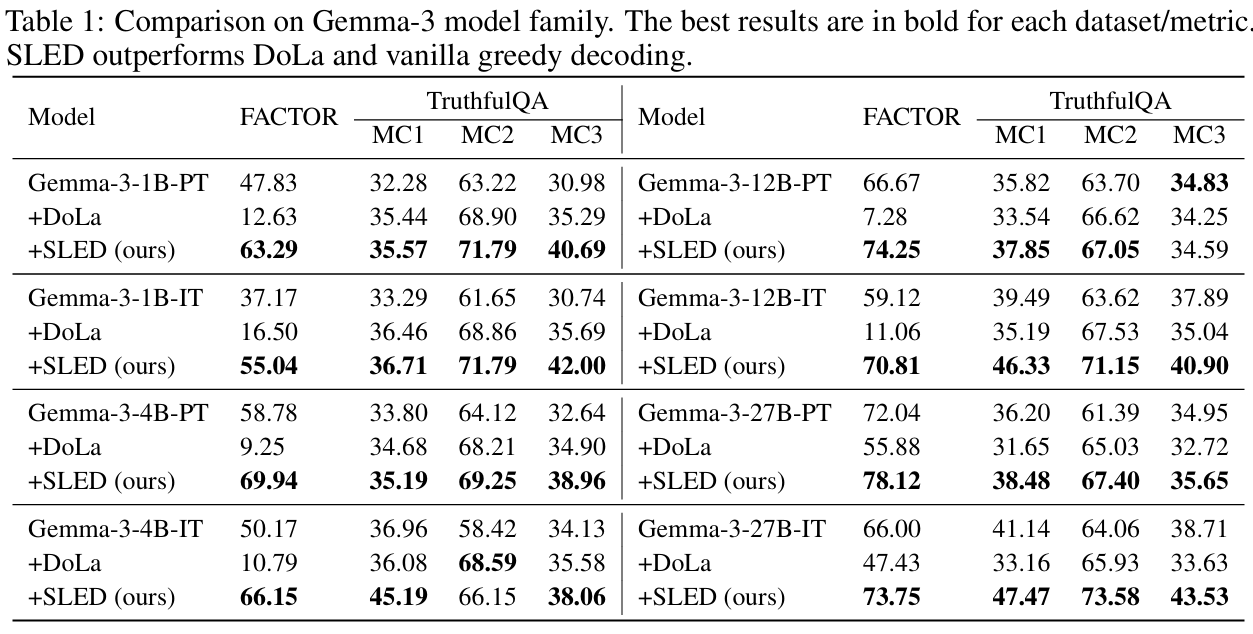
Table 1 summarizes these results: SLED outperforms greedy decoding and DoLa across most metrics and scales, with especially notable improvements on the more sensitive MC1 and MC3 scores. For long-form answers in FACTOR, the authors report gains in the range of roughly 5 to 13 percent compared to baselines (Zhang et al., 2024), (Lin et al., 2022), (Muhlgay et al., 2023).

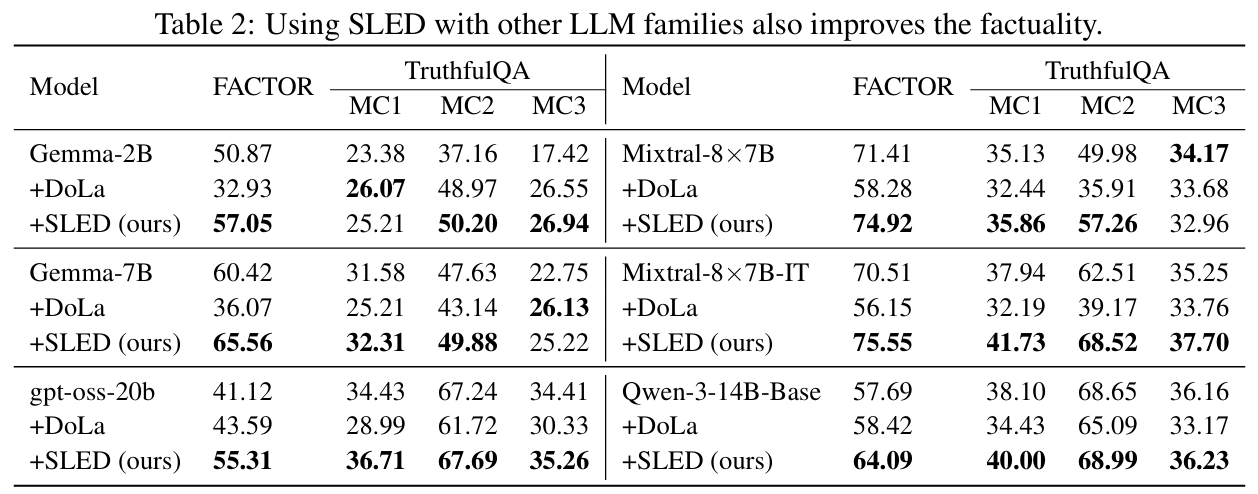
Beyond Gemma-3, Table 2 shows the method applied to Mixtral-8x7B and its instruction-tuned variant, to a Qwen-3 base model, and to a gpt-oss-20b model. The reported results continue the trend: SLED typically surpasses both greedy and DoLa, suggesting that the layer-aggregation and gradient-like update generalize across architectures, including MoE systems (Jiang et al., 2024), (Yang et al., 2025).

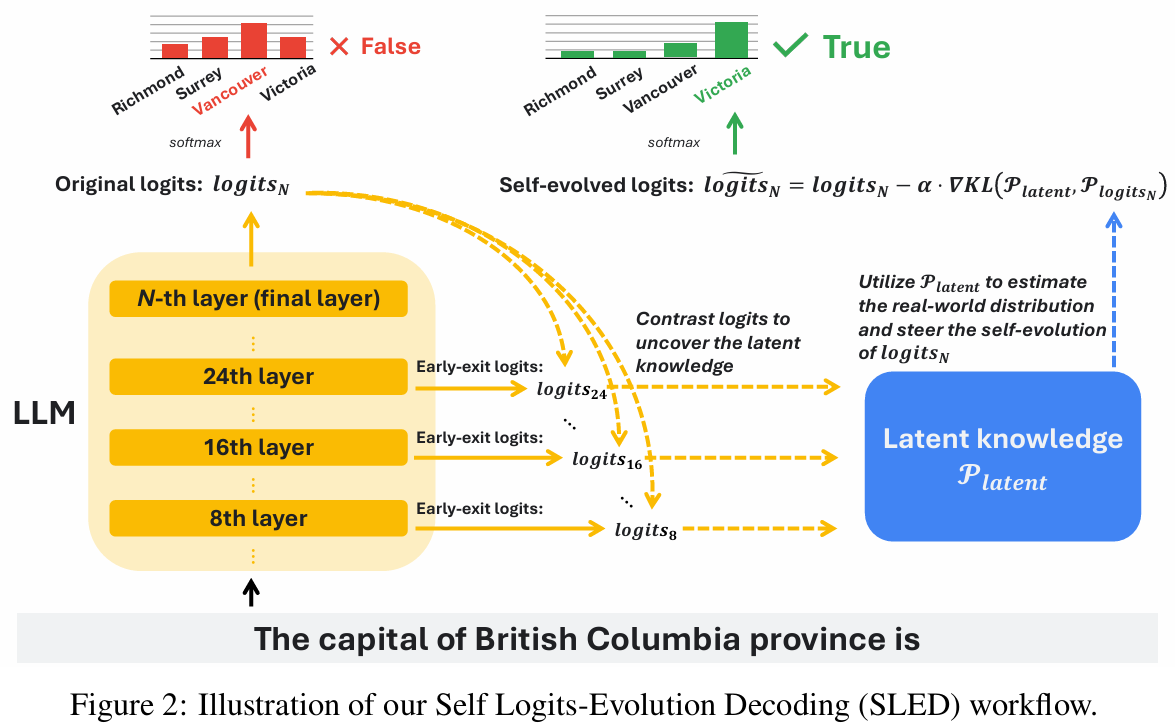
Figures in the paper help unpack how and why the method works. Figure 2 illustrates the core workflow: starting from final-layer logits, estimate a latent target by contrasting with early layers, then perform a one-step update that reduces KL divergence with the latent target, and finally sample from the adjusted distribution. 

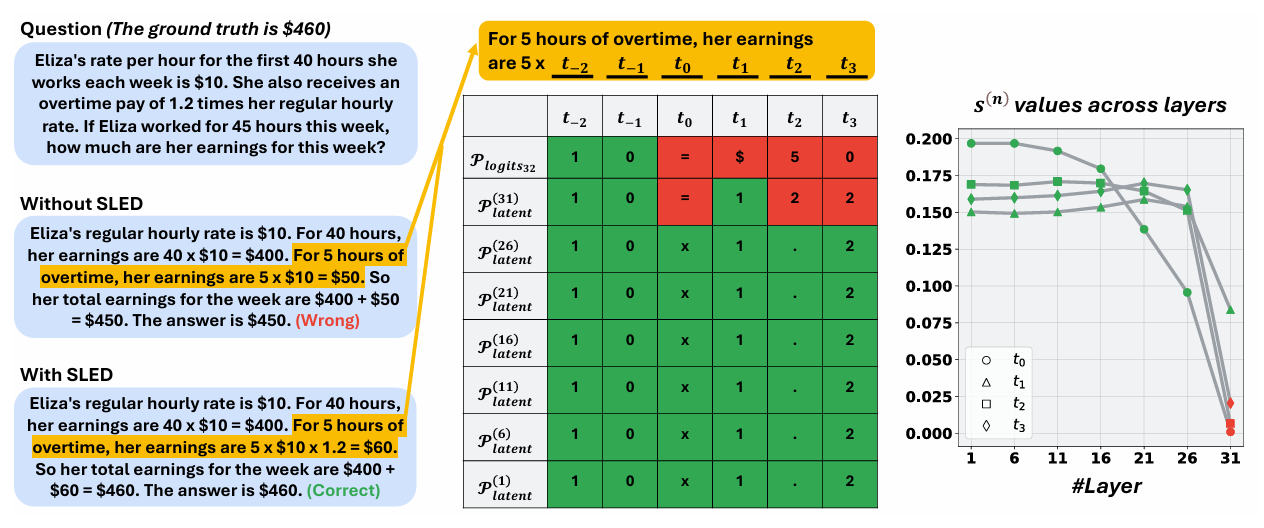
Figure 3: An example from GSM8K demonstrating SLED’s mechanism. SLED derives the estimations $P_{\mathrm{latent}}^{(n)}$ by contrasting the final layer’s logits ${\mathrm{logits}}_N$ with early layers’ logits $\{{\mathrm{logits}}_n\}$. We list the token with the highest probability value from each $P_{\mathrm{latent}}^{(n)}$ for different early layers. As shown, SLED downplays incorrect tokens by assigning lower weights $s^{(n)}$ to the corresponding $P_{\mathrm{latent}}^{(n)}$. Conversely, if the estimation is correct, the weights $s^{(n)}$ are relatively larger. The parameter evolution scale is set to $k=2$.

Figure 3 provides a GSM8K example that visualizes per-layer latent distributions and layer weights. When early layers overemphasize an incorrect token, SLED assigns that layer a smaller weight in the ensemble. Layers that align with the correct token receive larger weights. This alignment-aware weighting explains why aggregating across layers is more robust than choosing a single premature layer.

Latency is an important practical dimension. The project page reports negligible additional decoding time for SLED relative to DoLa, typically in the 0.1 to 10 percent range even with a large evolution scale. This aligns with the paper's complexity analysis: by restricting to a small top-k set and doing a single update step, SLED avoids heavy compute while focusing on the most plausible tokens (Project Website).

The authors also emphasize compatibility. Because SLED only manipulates logits layer-wise at inference, it composes with other techniques. The project page documents improvements when combined with inference-time intervention, activation-level strategies, and contrastive decoding. While the paper does not claim universal gains under every configuration, the general pattern is that SLED introduces a principled, low-cost signal that can steer outputs toward truth without sacrificing fluency.

Limitations And Open Questions

SLED treats early-layer signals as a proxy for the true distribution. When those signals are systematically biased - for example, due to pretraining artifacts or domain shift - the latent target may still be misled. 

The step-size parameter mitigates but does not eliminate this risk. In high-stakes or domain-specific deployments, combining SLED with retrieval or human-in-the-loop checks remains prudent (Zhang et al., 2023), (Huang et al., 2023).

The method also assumes access to intermediate layer logits, which are available in most open models but may be restricted in some hosted APIs. Finally, choosing k and $\alpha$ involves task-dependent trade-offs between stability, compute, and degree of correction. The paper's ablations suggest robustness, but there is room to study adaptive schedules for k and $\alpha$ that respond to uncertainty in real time.

Conclusion

SLED reframes inference-time decoding as a small, targeted optimization step that aligns the final distribution with a latent target distilled from earlier layers. The result is a practical boost in factuality across models and tasks - without extra training or external knowledge - and with minimal latency penalty. For practitioners, it is a compelling default to try when factuality matters and retraining is off the table. 

For researchers, the optimization lens clarifies why layer-contrastive signals help and invites further work on adaptive step sizes, uncertainty-aware weighting, and integration with retrieval or supervision.

Read the paper and browse figures, results tables, and code via the official project page (Project Website) and the arXiv preprint (Zhang et al., 2024). Baselines and related methods referenced include DoLa (Chuang et al., 2024), Contrastive Decoding (Li et al., 2022), and Inference-Time Intervention (Li et al., 2023). Benchmarks include TruthfulQA (Lin et al., 2022) and FACTOR (Muhlgay et al., 2023). Model family reports referenced: Mixtral (Jiang et al., 2024), Gemma 3 (Gemma Team, 2025), and Qwen 3 (Yang et al., 2025).

Definitions

Logits: Pre-softmax scores over the vocabulary. The softmax converts logits to probabilities as $p_i=\exp ({\ell }_i/\tau )/\sum _j\exp ({\ell }_j/\tau )$.

KL divergence: A measure of how one probability distribution differs from another. Here SLED minimizes $\mathrm{KL}(P_{\text{latent}},P_{{\text{logits}}_N})$ via a one-step update of final logits.

Evolution rate $\alpha$: Step size used to update final logits toward the latent target.

Evolution scale k: The number of top tokens considered for explicit update. Others are assigned very low logits to reduce compute and noise.

Temperature $\tau$: Scales the logits before softmax, controlling output distribution sharpness and the update magnitude.