Scaling Laws Unveiled: The Mathematical Blueprint Behind Smarter, Cheaper AI Models

Training a state-of-the-art language model can cost tens of millions of dollars and months of computation time, not to mention the expertise needed for development. Yet until now, researchers have been making these massive investments with limited ability to predict whether their approach will succeed. What if there was a way to forecast the performance of a large parameter model by training only smaller, cheaper versions?

This is exactly what a team of researchers from MIT and IBM Research has accomplished in their study, "A Hitchhiker's Guide to Scaling Law Estimation." Their work represents the most comprehensive analysis conducted to date on predicting large language model performance, potentially revolutionizing how organizations approach AI development and saving the industry billions in computational costs.

Decoding the Science of Scaling Laws

Machine learning researchers have long known that bigger models tend to perform better, but understanding exactly how to scale them efficiently has remained a challenge. A new study by researchers from MIT and IBM Research provides the most comprehensive analysis to date on how to predict large language model performance. Published in the Proceedings of the 42nd International Conference on Machine Learning, this research offers practical guidance that could save organizations compute costs while making AI development more accessible.

Led by Leshem Choshen from MIT, Yang Zhang from IBM Research, and Jacob Andreas from MIT, the team collected and analyzed training data from 485 previously published models to estimate over 1,000 scaling laws. Their findings challenge several conventional assumptions about model training and provide concrete recommendations for more efficient scaling law estimation.

Key Takeaways

• Using intermediate training checkpoints instead of only final model performance can substantially improve scaling law accuracy
  
  
• Training multiple smaller models often provides better predictions than training a single large model due to reduced variance
  
  
• Scaling laws estimated from models of similar sizes are generally more accurate, but predictions can still be reliable when extrapolating to much larger models
  
  
• The first 30% of a training run provides enough information to predict final performance with reasonable accuracy
  
  
• Current language model families are similar enough that scaling parameters can sometimes be borrowed between different architectures
  
  
• A minimum absolute relative error of 4% represents the practical limit for scaling law accuracy due to inherent training variance

Understanding Scaling Laws Fundamentals

Scaling laws are mathematical relationships that describe how a language model's performance changes based on the number of parameters it contains and the amount of training data it sees. Think of them as predictive formulas that help researchers estimate whether doubling a model's size or training dataset will lead to proportional improvements in performance. 

The mathematical foundation was established by Kaplan et al. (2020) at OpenAI, who first demonstrated that model performance follows power laws across model size, dataset size, and compute budget. Their seminal work revealed that loss scales predictably across more than seven orders of magnitude.

The field experienced a significant mathematical refinement with the Hoffmann et al. (2022) Chinchilla study, which corrected key assumptions in the original Kaplan scaling laws. While Kaplan's work suggested that very large models should be trained on relatively modest datasets, Hoffmann demonstrated that optimal training requires approximately equal scaling of parameters and training tokens, a finding that revealed models like GPT-3 to be significantly undertrained rather than optimally scaled. This correction fundamentally changed how the field approaches compute allocation for large language models.

However, estimating these scaling laws accurately has remained more art than science. Previous research typically involved training separate models for each data point, making the process expensive and time-consuming. 

The mathematical challenge lies not just in fitting power laws to data, but in determining which data points to include, how to handle training dynamics, and when scaling relationships generalize across different model architectures and training procedures. The new study reveals that this approach, while thorough, may not be the most efficient or accurate method for predicting large-scale model behavior.

Extracted Q&A From the Paper

The authors structure their paper in the form of question and extended answers. Here we have collected up the areas addressed by this research for brevity.

4. How well should scaling laws predict? 4% is the best ARE typically obtained; ARE up to 20% can still distinguish between many modeling choices.

5. When I train a new model, do I even need a new scaling law? Different model families exhibit different scaling behavior, but performance can sometimes be estimated using a single model in a new family.

5.1. Can I train the target model a bit instead of many small models? Yes, but obtaining reliable estimates in this way requires up to 30% of the full training run.

5.2. Are even simpler baselines enough? Some extrapolation is necessary: scaling laws can produce accurate estimates even when the target model vastly outperforms any training model.

6. I have some data; what portions should I use? Estimate scaling laws from intermediate checkpoints, not just fully trained models!

6.1. Should I use all intermediate checkpoints? Almost all, but drop very early checkpoints.

7. How big a model should I train? Larger models are better, but not necessary. Mainly, beware of specific models that might give noisy results.

8. How many models for reliable predictions? 5 models is a safe bet, more would improve the results' robustness. These models can be small.

9. Are all scaling law parameters crucial? Scaling laws might have fewer degrees of freedom than described in the literature.

C. Is scaling working only upwards? No. Small models usually show consistent and predictable performance. The text suggests that predicting smaller models from larger ones can be a useful baseline and that the number of models used for the prediction is important.

D. Can we detect bad models to fit on? If so, not through cross-validation. The authors hypothesized they could identify "bad" models (those that skew predictions) by seeing which ones were hard to predict via cross-validation. This hypothesis was found to be incorrect.

Exploring the Mathematical Framework

At the heart of this research lies a precise mathematical formulation that builds upon the foundational work of Kaplan et al. (2020). The study employs the refined Hoffmann scaling law from Hoffmann et al. (2022), which corrected Kaplan's original findings by showing that optimal training requires equal scaling of both parameters and data. The mathematical relationship takes the form:

$$\hat{L}(f)=e^E+\frac{e^A}{\text{\#params}(f{)}^{\alpha }}+\frac{e^B}{\text{\#toks}(f{)}^{\beta }}$$

This formulation represents a significant evolution from earlier scaling laws. Kaplan's original work established that loss scales as power laws with model size and dataset size independently, but Hoffmann's Chinchilla study revealed that previous large models like GPT-3 were severely undertrained. 

The Hoffmann parameterization captures this insight by modeling the loss as a sum of three terms: a baseline model performance floor $e^E$, a parameter-dependent (model size error) term that decreases as the number of parameters increases $\text{\#params}(f{)}^{-\alpha }$ , and a data-dependent term that decreases as the number of training tokens increases, $\text{\#toks}(f{)}^{-\beta }$.

The current study's most significant mathematical discovery concerns the parameter optimization process itself. The researchers employ scipy's curve_fit function with standard least-squares minimization to estimate the five parameters by solving: $$\underset{E,A,\alpha ,B,\beta }{min}\sum _{f\in F_{\text{train}}}{(\hat{L}(f)-L(f))}^2$$ where L(f) denotes the empirical negative log-likelihood of some held-out data under the model f. 

They also experimented with L-BFGS optimization and Huber loss for robustness, finding that while these methods occasionally provided different parameter estimates, the predictive accuracy remained consistent across optimization approaches.

Through principal component analysis of the learned parameters across 40+ model families, the researchers uncovered a fundamental mathematical structure: just three principal components explain 99.49% of the variance in the five-dimensional parameter space. 

This dimensional reduction reveals that the parameters $(A,\alpha )$ and $(B,\beta )$ are strongly correlated within each pair, despite their nonlinear interaction in the scaling law equation. See figure 3 below for plots.

Mathematically, this suggests the existence of underlying constraints that reduce the effective degrees of freedom from five to approximately three, indicating potential over-parameterization in current scaling law formulations.

Statistical Methodology

The mathematical rigor of this study extends beyond the scaling law formulation to encompass sophisticated statistical methodologies for parameter estimation and validation. The researchers employ a carefully designed train-test split strategy, using all models except the largest in each family for parameter estimation ($F_{\text{train}}=F\setminus F_{\text{max P}}$), then evaluating predictions on the largest models using the final 30% of their training checkpoints : $F_{\text{target}}=F_{\text{max P}}\cap F_{\text{\#tok>30\%}}$

The choice of evaluation metric (Absolute Relative Error (ARE)) provides mathematically meaningful comparisons across model families with vastly different loss scales. The ARE is defined as the absolute error between the empirical loss L and the loss $\hat{L}$ predicted by the scaling law. : $$ARE={\mathbb{E}}_{f\in F_{target}}|L(f)-\hat{L}(f|F_{train})|/L(f)$$ 

This relative measure ensures that prediction errors are comparable whether evaluating a 70M parameter model with loss 3.5 or a 70B parameter model with loss 2.1, avoiding the scale bias that would plague absolute error metrics.

The study's statistical robustness extends to investigating alternative optimization approaches. While the primary results use scipy's curve_fit with least-squares loss, the researchers validated their findings using L-BFGS optimization and Huber loss for outlier robustness. The consistency of results across these different mathematical optimization approaches strengthens confidence in the underlying scaling relationships and demonstrates that the discovered patterns are not artifacts of particular methods.

Perhaps most importantly, the researchers establish fundamental statistical limits on scaling law accuracy through careful analysis of training variance. They demonstrate that even identical model configurations exhibit performance differences of up to 3.5% due to random initialization and optimization stochasticity, establishing an irreducible lower bound on prediction accuracy. 

This finding provides crucial mathematical context for interpreting scaling law performance, the observed 4% ARE limit represents the practical boundary imposed by inherent randomness in neural network training, not methodological limitations.

Methodology Breakthrough

The researchers' most significant finding challenges a fundamental assumption in scaling law research: that only fully trained models provide useful data points. Traditional approaches have treated each training run as producing a single useful measurement at completion, but this study demonstrates that intermediate checkpoints throughout training contain valuable information that dramatically improves scaling law accuracy.

By analyzing training trajectories rather than just final outcomes, the team discovered that scaling laws fitted to intermediate checkpoints predict final losses significantly better than those based solely on completed training runs. This approach effectively multiplies the amount of useful data available from each training experiment, making scaling law estimation both more accurate and more cost-effective.

The methodology breakthrough extends beyond simple data collection improvements. The researchers found that the very beginning of training runs (roughly the first 10% of tokens) can actually harm scaling law predictions and should be excluded from analysis. This insight aligns with known phenomena in neural network training, where early training phases often exhibit instability and poor generalization of scaling behavior.

Perhaps most importantly, the study reveals that training multiple smaller models provides more robust scaling law estimates than training fewer larger models. This counterintuitive finding stems from the inherent variance in large model training, where individual models can exhibit unexpectedly high or low performance that skews predictions. By diversifying across multiple smaller experiments, researchers can achieve more reliable estimates while consuming fewer computational resources.

Practical Implications for Industry

The practical applications of this research extend far beyond academic curiosity. For organizations developing large language models, these findings could translate into substantial cost savings and more informed decision-making. 

Consider this scenario: instead of spending $50 million to train a 175-billion-parameter model from scratch, a company could now predict its performance by training several smaller models for perhaps $5-10 million total. The ability to predict model performance from partial training runs means companies can make go/no-go decisions earlier in the development process, potentially saving millions of dollars in computational costs and reducing environmental footprints.

The research also demonstrates that scaling laws can sometimes be transferred between different model families. In some cases, researchers found that parameters estimated from one architectural family (such as GPT models) could be applied to predict the behavior of different architectures (such as T5 models) with reasonable accuracy. This cross-family transfer capability could accelerate research in new model architectures by leveraging existing scaling law knowledge.

For smaller research teams and organizations with limited computational budgets, the findings are particularly valuable. The study shows that meaningful scaling law estimates can be obtained from training just 3-5 smaller models, making scaling law research accessible to a broader range of researchers. This democratization of scaling law estimation could accelerate innovation across the field by enabling more teams to make informed scaling decisions.

Experimental Analysis

The researchers' experimental approach represents the largest-scale meta-analysis of scaling laws ever conducted. Their dataset encompasses 1.9 million training steps across 485 unique pretrained models from 40 different scaled families, including popular models like Pythia, OPT, OLMO, and LLaMA. This comprehensive scope allows for unprecedented insights into scaling behavior across different architectures, datasets, and training configurations.

The analysis revealed that achieving an absolute relative error (ARE) of 4% represents the practical limit for scaling law accuracy. This limitation stems not from methodological shortcomings but from inherent variance in neural network training. Even identical model configurations can exhibit performance differences of up to 3.5% due to random initialization and optimization dynamics, establishing a fundamental lower bound on prediction accuracy. To put this in perspective, many published modeling improvements claim benefits of 4-50%, making 4% accuracy sufficient to distinguish between meaningful advances.

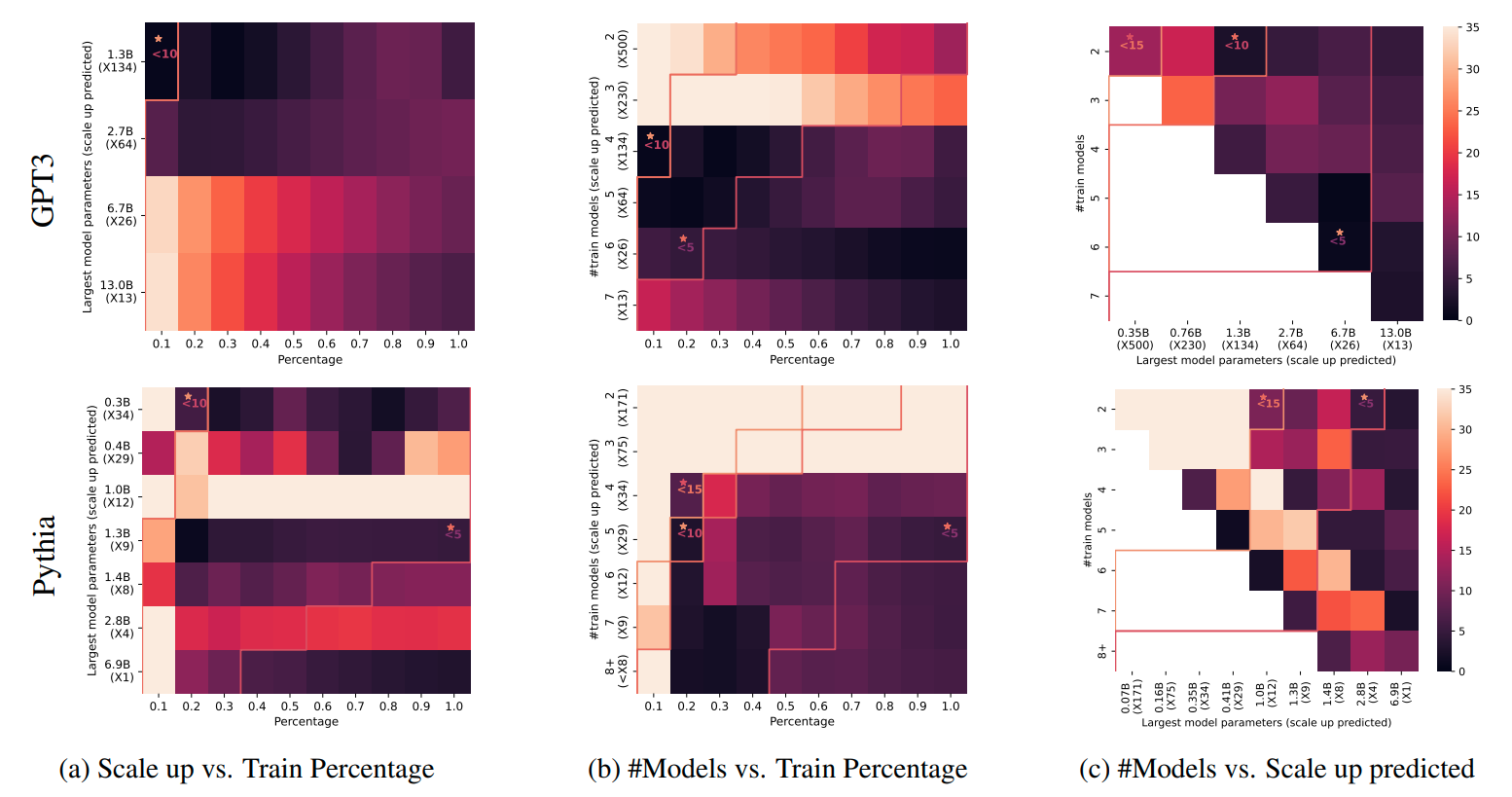
Figure 2: The effects of 3 variables on scaling law accuracy. Each cell corresponds to a single scaling law estimated from a set of model checkpoints $F_{t}rain$, with the color denoting the error when predicting the largest model. Each column shows a subset of the three axes along which these training sets differ: (1) the number of tokens used to train each LM in $F_{t}rain$ (expressed as a fraction of the full training corpus), (2) the number of distinct models trained; and (3) the size of the largest model trained (expressed as a scale-up factor—the ratio between the target model and the largest model in $F_{t}rain$). In (a), all laws are estimated from four models. In (c) all laws use the full corpus. Orange lines show iso-FLOP contours (sets of scaling laws whose training sets require the same computational cost to produce). represent the most efficient ways to obtain 15%, 10% and 5% ARE. One of the most immediate conclusions from these plots is that scaling law estimation is quite noisy—the inclusion of a single badly-behaved model in the estimation procedure can produce large errors, and in small model families error does not reliably decrease with additional computation. However—because of noise—it is often preferable to extrapolate from a large number of small, partially trained models rather than a small number of large models.

Figure 2 in the paper provides particularly compelling evidence for the researchers' recommendations. The visualization shows how three key variables affect scaling law accuracy: the number of training tokens used for each model, the number of distinct models trained, and the size of the largest model relative to the target. The results clearly demonstrate that using more models and more training data consistently improves predictions, while the effect of training larger individual models is less pronounced and sometimes counterproductive due to increased variance.

The study also investigates whether simple baseline approaches might suffice for scaling law estimation. By comparing their fitted scaling laws against pessimistic baselines that assume no improvement beyond the best observed model, the researchers confirm that proper scaling law fitting provides substantial value. The baselines consistently achieved errors above 15%, while well-fitted scaling laws regularly achieved errors below 5%.

Mathematical Insights and Innovations

Beyond practical recommendations, the research provides important theoretical insights into the mathematical structure of scaling laws themselves. The team's analysis suggests that scaling laws may have fewer degrees of freedom than typically assumed in the literature.

Through principal component analysis of learned parameters across different model families, they found that just three components explain 99.49% of the variance in the five standard scaling law parameters, a finding that challenges the conventional assumption of parameter independence.

Figure 3: Parameters differ between scaled model families. Surprisingly, however, the pairs of parameters controlling the influence of model and training set size have similar ratios. The legend shows model architecture (left), scaling families (center) and per-family intercept (right).

This dimensional reduction reveals fundamental mathematical constraints within the scaling law framework. The tight coupling between parameter pairs $(A,\alpha )$ and $(B,\beta )$ suggests that the relationship between scaling magnitude and exponent is not arbitrary but follows underlying mathematical principles. In practical terms, this means that if you know how adding parameters affects performance in one model family, you can often predict this relationship in other families. This mathematical insight builds upon the theoretical foundations laid by Kaplan et al. (2020), who first identified power law relationships in neural scaling, but extends them by revealing the interconnected nature of scaling parameters.

The analysis also reveals interesting architectural dependencies in scaling behavior. Encoder-decoder models like T5 exhibit different scaling parameter relationships compared to decoder-only transformers, suggesting that architectural choices can introduce systematic biases in the relationships. Additionally, models trained with multiple passes over the same dataset show distinct parameter correlations, indicating that the optimization dynamics during training affect the emergent structure of scaling laws.

The researchers identify specific mathematical exceptions that shed light on the boundaries of scaling laws. Four model families trained with multiple epochs show deviation from the standard parameter correlation patterns, while encoder-decoder architectures consistently exhibit different $B$ vs. $\beta$ relationships. These exceptions provide valuable constraints for understanding when scaling laws can be transferred between model families and when new estimation procedures are required.

The mathematical insights extend to optimization methodology itself. The study demonstrates that the choice of loss function (least squares vs. Huber loss) and optimization algorithm (curve_fit vs. L-BFGS) affects parameter estimates but remarkably preserves predictive accuracy. This robustness suggests that the underlying mathematical relationships captured by scaling laws are fundamental rather than artifacts of particular optimization procedures, lending credibility to the transferability findings.

Finally, the research opens important questions about alternative mathematical formulations. While the study primarily uses the Hoffmann et al. parameterization, the observed parameter correlations suggest that simpler functional forms might achieve equivalent predictive power. The authors explicitly call for future work to explore constrained optimization approaches that leverage the discovered parameter relationships, potentially leading to more elegant and computationally efficient scaling laws.

Broader Implications for Future Research

The implications of this work extend well beyond immediate practical applications to fundamental questions about how we understand and predict neural network behavior. The success of intermediate checkpoint analysis suggests that training dynamics contain more information than previously recognized, opening new avenues for research into training efficiency and optimization strategies.

The finding that scaling laws can sometimes transfer between model families challenges the conventional wisdom that each new architecture requires completely independent scaling analysis. This transferability could accelerate research into novel architectures by providing starting points for scaling law estimation rather than requiring complete re-derivation from scratch.

The research also highlights the importance of variance and uncertainty in scaling law estimation, areas that have received relatively little attention in the literature. The finding that training multiple smaller models often outperforms training fewer larger models runs counter to intuitive expectations and suggests that the field's focus on ever-larger individual experiments may not always be optimal.

Looking forward, the study opens several promising research directions. Researchers suggest investigating scaling laws for training efficiency metrics beyond loss, exploring how architectural innovations affect scaling behavior, and developing more sophisticated methods for detecting and handling outlier models that skew scaling law estimates.

Implementation Recommendations

For researchers looking to apply these findings, the paper provides specific, actionable recommendations. When estimating scaling laws with limited computational budget, the authors recommend training 5 or more models of varying sizes rather than focusing resources on a single large model. This approach provides better estimates due to reduced variance while requiring less total computation.

The timing recommendations are equally practical: useful scaling law estimates can be obtained after training models for approximately 30% of their intended duration. This allows for early stopping of unpromising experiments while still gathering valuable data for scaling law estimation. However, researchers should exclude the very beginning of training runs (roughly the first 10% of tokens) from their analysis due to training instabilities.

For organizations with extremely limited budgets, the research demonstrates that meaningful predictions can sometimes be obtained from a single partially-trained model in the target family, combined with scaling parameters borrowed from other families. While this approach sacrifices some accuracy, it can provide valuable guidance when full scaling law estimation is not feasible.

Specific guidance on data collection and preprocessing is also provided. They recommend using all available intermediate checkpoints (except early training phases), fitting scaling laws with standard least-squares methods, and carefully validating results against held-out test data from the final stages of training runs.

Looking Ahead: Challenges and Future Directions

While this research represents a significant advance in scaling law methodology, several important challenges remain. The authors acknowledge that their primary metric, absolute relative error, does not distinguish between over- and under-estimation of performance. This limitation could be particularly important when using scaling laws to choose between competing model architectures or training strategies.

The difficulty of aggregating information across diverse model families also presents ongoing challenges. Different model families often operate at incomparable scales and over different performance ranges, making it difficult to derive universal scaling law principles that apply across all architectures and training regimes.

Future research directions include extending scaling law analysis to downstream task performance rather than just training loss, developing methods for handling limited data scenarios (such as rare languages where training data is scarce), and exploring scaling laws for emerging model architectures like mixture-of-experts systems and multimodal models.

The authors also call for greater data sharing within the research community. Their work was enabled by the availability of training data from multiple research groups, and they encourage other teams to share training trajectories and evaluation results to enable more comprehensive scaling law research. Such sharing could accelerate progress across the entire field while reducing redundant computational effort.

The Path Forward: Democratizing AI Development

The MIT and IBM Research team's work represents a blueprint for making AI development more efficient, accessible, and cost-effective. By showing that scaling laws can be estimated from intermediate checkpoints and smaller models, they've potentially democratized access to large-scale AI development, enabling smaller teams and organizations to make informed decisions with reduced risk and computational costs.

This research provides the foundation for more strategic AI development, where resources can be allocated based on solid predictive models rather than expensive trial-and-error approaches. As the field continues to push toward ever-larger models, these insights will become increasingly valuable for navigating the complex landscape of AI scaling decisions.

For researchers and practitioners, the message is clear: the next breakthrough in your AI project might not require the largest possible model, it might simply require smarter scaling law estimation. The hitchhiker's guide has arrived, and it's pointing toward a more efficient future for artificial intelligence development.

What are your thoughts on this scaling law breakthrough? Have you encountered similar challenges in predicting model performance in your work? Share your experiences and insights in the comments below, and explore the full dataset and code to start applying these techniques in your own research.

Definitions

Scaling Law: A mathematical relationship that describes how neural network performance changes as key factors like model size, training data, or computational budget are increased or decreased.

Absolute Relative Error (ARE): A metric for measuring scaling law accuracy, calculated as the absolute difference between predicted and actual performance divided by actual performance, typically expressed as a percentage.

Model Family: A set of neural networks that share the same architecture and training methodology but differ in size (number of parameters) and training data amount.

Intermediate Checkpoints: Saved model states captured during training at regular intervals, allowing researchers to analyze performance throughout the training process rather than just at completion.

Parameter Count: The total number of learnable parameters (weights and biases) in a neural network, typically measured in millions (M) or billions (B).

Training Tokens: The total number of individual text pieces (words, subwords, or characters) that a language model processes during training, typically measured in billions or trillions.

Chinchilla Scaling: A specific scaling law formulation that suggests optimal performance requires equal scaling of both model parameters and training data size with computational budget.

Perplexity: A measure of how well a language model predicts text, with lower values indicating better performance. Related to the exponential of the average negative log-likelihood per token.