How Direct Reasoning Optimization Teaches LLMs to Grade Their Own Thinking

Large language models have learned to reason well in math and coding thanks to reinforcement learning with verifiable rewards, where an answer can be checked automatically. Open-ended tasks like rewriting a paragraph based on reviewer comments are harder: there is often no single correct output and naive string-similarity rewards can be gamed. 

A new paper from Microsoft and UCLA introduces Direct Reasoning Optimization (DRO), which uses a model’s own token-level certainty over a reference outcome to reward the parts of the output that actually reflect good chain-of-thought. 

The core signal, called the Reasoning Reflection Reward (R3), claims to fix a known pitfall in log-probability aggregation for long text, and to reduce training cost while improving quality on both open-ended writing (ParaRev) and a math-like benchmark (FinQA).

In this article I take a look at how R3 works, what DRO changes relative to standard RLVR recipes, and what the experiments really show.

​

Key Takeaways

• R3 is a token-level, model-internal reward that up-weights tokens in the reference answer most sensitive to the model’s preceding chain-of-thought, avoiding dilution from uninformative tokens.
  
  
• DRO plugs R3 into GRPO-style training and adds R3-driven data filtering, cutting training cost on ParaRev by about 45% while improving win rates over GPT-4o.
  
  
• On ParaRev, DRO-R3 beats strong baselines, including versions trained with ROUGE or simple aggregate certainty; it achieves 51.8% (GPT judge) and 58.8% (Claude judge) win rates versus GPT-4o, with more faithful edit lengths (Table 1).
  
  
• On FinQA, DRO-R3 matches or slightly trails binary correctness at Pass@1 but surpasses it at higher Pass@k, showing R3 also works when outcomes are verifiable (Table 2; Chen et al., 2021).
  
  
• Figure analyses points to two problems R3 addresses: critical-token blindness under aggregate log-likelihood and spurious certainty propagation from previously appended reference tokens.

Overview

Reinforcement Learning with Verifiable Rewards (RLVR) has driven recent jumps in LLM reasoning for math and code because success is easy to check: match the numeric answer, pass unit tests, or select the right choice. 

Techniques like Group Relative Policy Optimization (GRPO) compare groups of sampled trajectories and normalize rewards to stabilize training (Shao et al., 2024). But applying the same idea to open-ended tasks is tricky: string overlap metrics (ROUGE) reward copying and superficial similarity, and general “LLM-as-judge” rewards introduce prompt and model sensitivities that can be exploited (Gu et al., 2024).

R3 reframes open-ended reward design around a simple observation that the model’s chain-of-thought is a latent prefix conditioning the final answer. If the reasoning is good, the model’s own likelihood of the correct reference output should rise in places where the reasoning truly matters. 

​

However, two failure modes break naive use of log-probs in long text:

1. First, most tokens in a long reference are uninformative with respect to reasoning quality. Aggregating log-likelihood across all tokens drowns out the few “reasoning-reflective” tokens that actually vary across reasoning traces. 
   
   
2. Second, once you append part of the reference during likelihood computation, downstream tokens become easy because earlier reference tokens act as hints, inflating the reward even for poor reasoning. The paper formalizes both observations and designs R3 to counter them.

Concretely, R3 samples multiple chain-of-thought traces for a prompt, computes token-level probabilities of the reference outcome conditioned on each trace and then weights each reference token’s contribution by its variance across traces. 

High-variance tokens are treated as “reflective” because they move the most when the reasoning changes. To curb certainty that comes from earlier appended reference tokens rather than from the reasoning itself, R3 either applies localized decay from reflective tokens or subtracts a masked-CoT baseline, isolating the reasoning-induced certainty.

DRO then uses R3 inside GRPO. Where rewards are computed by an internal policy derived from the same base model (reference policy, dynamically synced, or lagged). Because R3 scores reasoning but not the final completion, DRO applies a length penalty only to the final answer to discourage verbose postambles. 

Finally, DRO introduces dynamic, R3-guided data filtering. It drops questions that appear beyond the model’s current knowledge and prunes low-variation prompts that do not produce informative reasoning trajectories.

Why It Matters

Open-ended text tasks are where LLMs are most useful, yet most RL recipes rely on verifiable final outcomes. R3 offers a path to bring outcome-driven RL to tasks where no exact answer exists, without training a separate reward model or relying on brittle judges. That reduces annotation and engineering overhead and keeps the reward closer to the ground truth objective providing consistency between reasoning and a trusted reference outcome.

Beyond writing tasks, the token-sensitivity idea generalizes. Even in math-like settings, only certain tokens carry causal weight for reasoning quality. The FinQA results suggest that learning to focus reward on critical tokens can be as effective as binary correctness, sometimes better at higher sampling budgets. This supports a broader principle: dense, token-aware rewards can stabilize learning, prevent reasoning collapse, and transfer across domains that mix structured and unstructured outputs (Chen et al., 2021).

Discussion

On ParaRev, DRO with R3 delivers higher pairwise win rates than all reported baselines and even surpasses GPT-4o despite using smaller distilled Qwen models. Specifically, Table 1 reports 51.8% (GPT judge) and 58.8% (Claude judge) win rates for DRO-R3 versus 43.8%/48.6% for the base model and notably lower scores for ROUGE- or aggregate-certainty–driven variants. 

Output lengths under DRO-R3 track the human reference more closely, indicating edits are substantive rather than superficial. Dynamic, R3-guided data filtering further trims training time by about 45% with comparable final rewards, improving both efficiency and stability.

On FinQA, a math-like benchmark with verifiable answers, DRO-R3 is competitive with binary correctness at Pass@1 and exceeds it at higher Pass@k (Table 2). This suggests that token-sensitive attribution of reward can match the benefits of exact-verifier signals, and in sampling regimes with k≥2 it may better guide exploration than a single-bit correctness reward.

Across both tasks, aggregate certainty over all tokens underperforms R3. The evidence supports the paper’s premise that a small subset of “reasoning-reflective” tokens carries most of the causal signal for judging a chain-of-thought, and that emphasizing these tokens avoids the collapse behaviors observed with naive aggregation.

Experimental setup, datasets, and evaluation. 

The study evaluates two domains: 

(1) ParaRev, a long-form paragraph revision task built from scientific papers and reviewer comments, adapted with additional local paper context via CASIMIR to yield an approximately 4.8K-sample dataset with a 95/5 train–test split (Jourdan et al., 2025; Jourdan et al., 2024).

(2) FinQA, a numerical reasoning benchmark with expert-authored questions and answers, using the original train–test split and a 2% numeric tolerance for correctness (Chen et al., 2021).

Models are DeepSeek-R1-Distill-Qwen-14B for ParaRev and 7B for FinQA. Training uses GRPO with scaled rewards and a small entropy regularizer. Per prompt, the actor samples groups of 16 chain-of-thoughts with temperature 1.0 and top-p 0.95; maximum completion lengths are up to 8k–10k tokens to accommodate long reasoning and outputs. 

For ParaRev, the primary metric is pairwise win rate against GPT-4o using both GPT-4o and Claude Sonnet as judges to mitigate bias; for FinQA, the metric is Pass@k under the numeric tolerance. 

Baselines include the base model (no task RL), ROUGE-rewarded RL (ParaRev), aggregate-certainty rewards (DRO-Aggr), and correctness rewards (FinQA). Compute spans three nodes with 8×A100 GPUs each, and the stack includes TRL, DeepSpeed, and vLLM.

What the figures and tables show. 

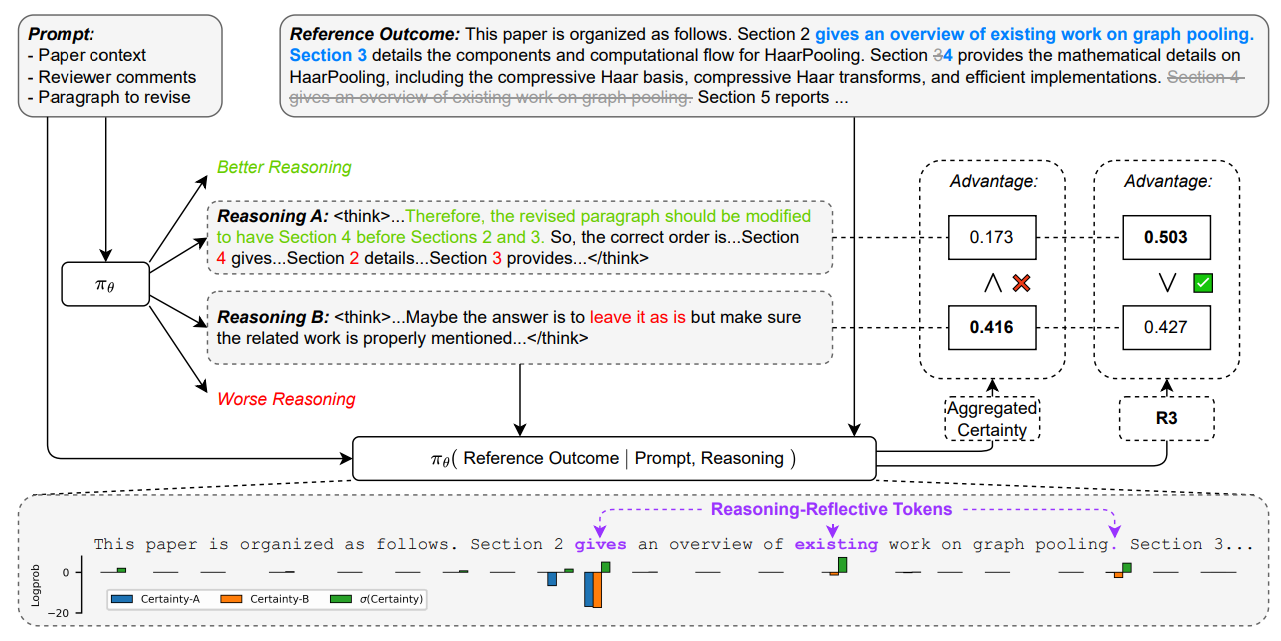
Figure 1: Illustrative example of Reasoning Reflection Reward (R3). For the paper revision task, the model is prompted to revise a paragraph based on reviewer comments (upper left). R3 computes per-token self-certainty (log-probabilities) in the reference revision (upper right) for each sampled reasoning trace, and highlights reasoning-reflective tokens using σ(certainty). In this example, Reasoning A correctly identifies that Section 4 (overview) has been moved earlier and adjusts the paragraph structure accordingly, with a minor omission of section numbers. Reasoning B gives up. While a vanilla aggregate of certainty prefers B over A due to A’s lower certainty on the token “2”, R3 successfully aligns with the desired ranking by up-weighting high-σ(certainty) tokens “gives”, “existing” and “.” that better reflect reasoning effectiveness. Credit: Xu et al.

Figure 1 illustrates the core pathology R3 addresses. When comparing two reasoning traces for the same ParaRev prompt, simple aggregation of token log-likelihoods mistakenly favors the worse trace because the few critical tokens that reflect reasoning quality are overwhelmed by many easy tokens. R3 re-weights by cross-trace variance to surface the reflective tokens (e.g., “gives,” “existing”), aligning the reward with human preference.

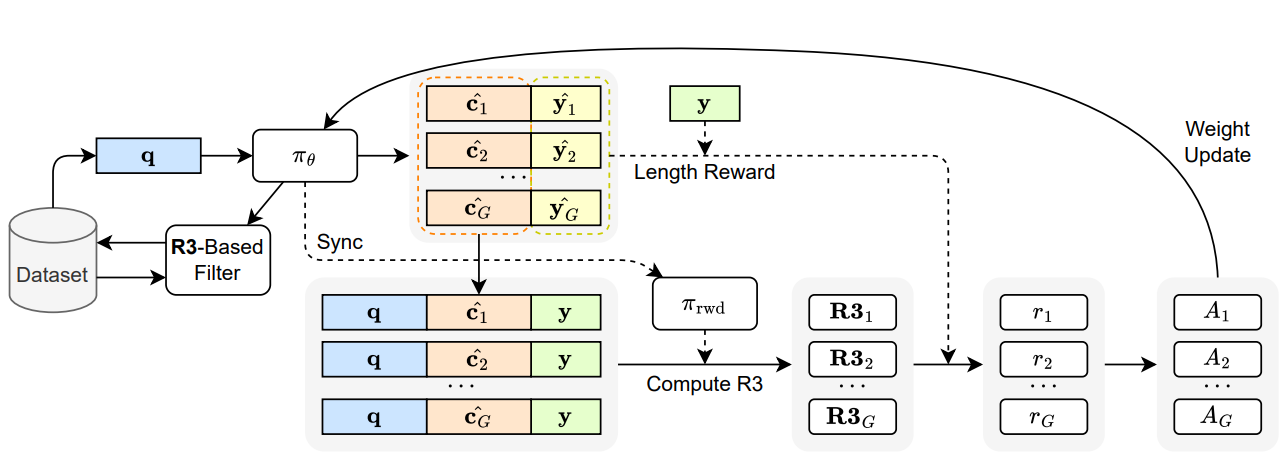
Figure 2: Overview of Direct Reasoning Optimization (DRO), a framework that rewards and refines reasoning by directly leveraging feedback from the training model. DRO operates within the GRPO framework, where a group of CoT reasoning traces sampled from the actor policy (πθ) are scored primarily using the R3 score along with length penalty on final outcome. The reward is computed via an internal policy (πrwd), derived from the same base reference policy (πref) being optimized. DRO employs R3-based dynamic training data filtering for open-ended reasoning tasks to improve data efficiency and downstream task performance. Credit: Xu et al.

Figure 2 depicts the DRO loop.  By sampling groups of chain-of-thoughts it the computes R3 using an internal policy tied to the reference model, applies a length penalty to the final outcome and updates with GRPO. The diagram also highlights dynamic, R3-based data filtering that prunes low-signal prompts during training.

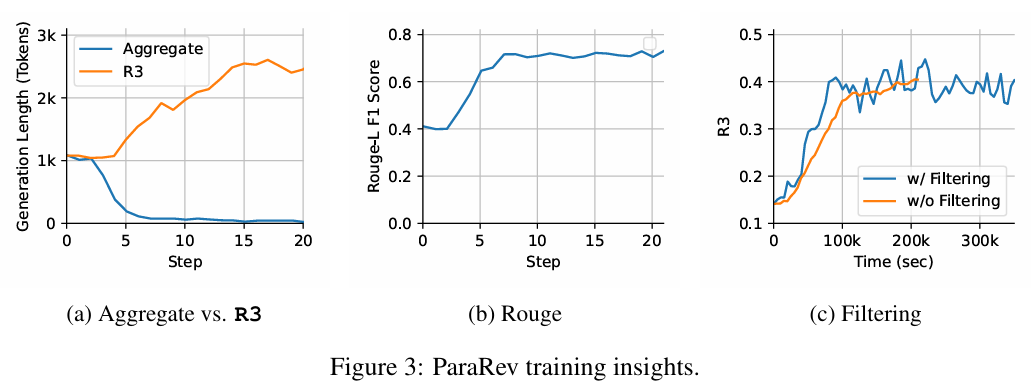
Figure 3 reports ParaRev training dynamics. Panel (a) shows chain-of-thought length: aggregate-certainty leads to rapid collapse below 100 tokens, whereas R3 steadily increases to over 2.5k, indicating healthier exploration. Panel (b) shows ROUGE-L improving despite not being rewarded, suggesting that optimizing reflective tokens yields better surface alignment as a byproduct. Panel (c) shows the on-the-fly filtering reducing wall-clock training time by about 45% while maintaining final reward and smoothing convergence.

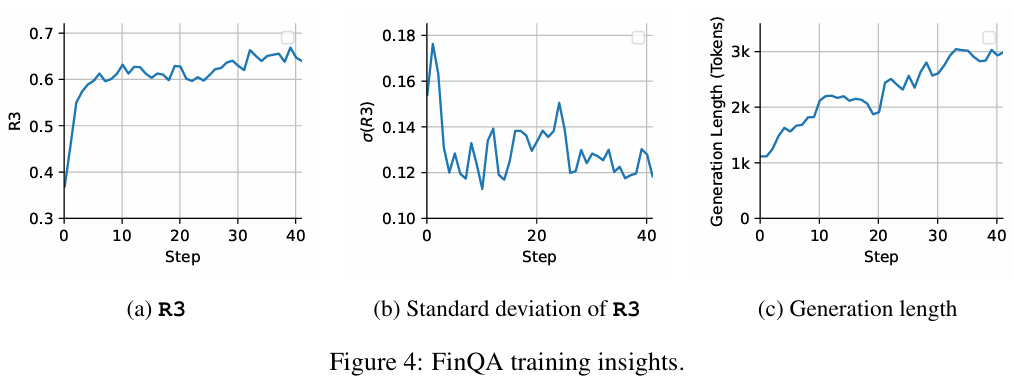
Figure 4 provides FinQA training insights. Panel (a) tracks the R3 reward rising across steps; Panel (b) shows its standard deviation shrinking, implying more stable attribution across sampled traces; Panel (c) shows continued growth in reasoning length from ~1k to >3k tokens even as reward gains begin to taper, suggesting the model continues to elaborate useful intermediate steps beyond what R3 directly incentivizes.

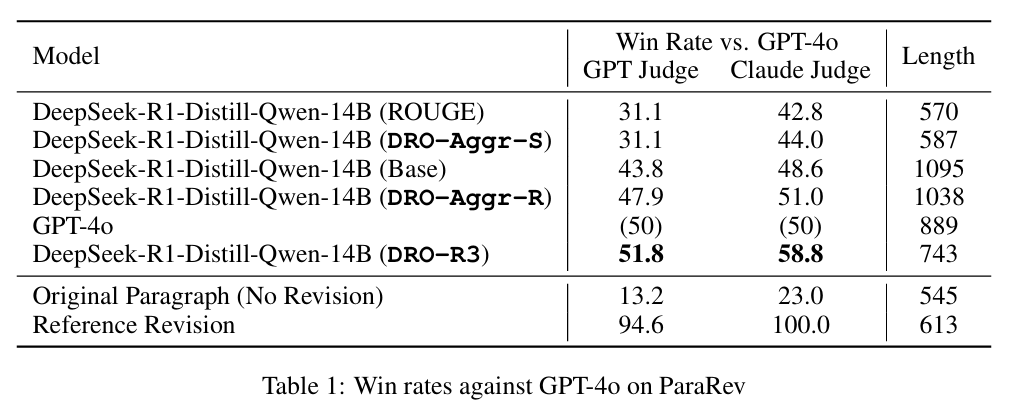
Table 1 quantifies ParaRev outcomes: DRO-R3 wins 51.8%/58.8% against GPT-4o (GPT/Claude judges), outperforming ROUGE-optimized and aggregate-certainty baselines and producing lengths closer to human references. 

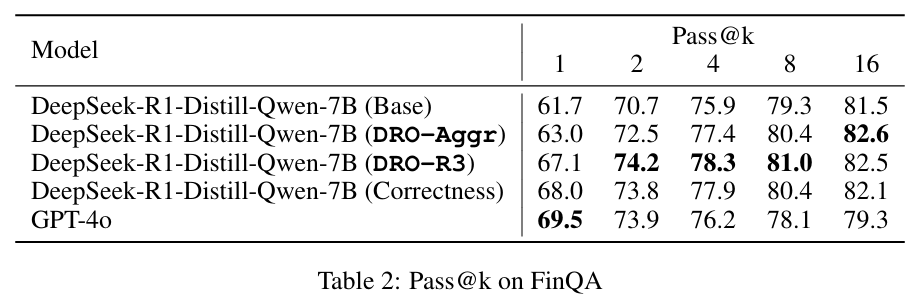
Table 2 quantifies FinQA: DRO-R3 achieves 67.1% Pass@1 and 74.2/78.3/81.0/82.5 at k=2/4/8/16, matching or surpassing correctness-based RL at k≥2 while exceeding the aggregate-certainty variant at lower k.

Limitations and caveats. 

R3 depends on reference outcomes. Where references are absent, a hybrid with verifiable subgoals or learned reward models may be needed. ParaRev win rates rely on LLM judges; despite dual-judge mitigation, residual biases are possible (Zheng et al., 2023; Gu et al., 2024). The approach uses long contexts and significant compute, which may limit accessibility; and R3 introduces weighting/decay hyperparameters that could require tuning across tasks.

Conclusion

Direct Reasoning Optimization proposes a practical way to reward what matters in open-ended tasks: the tokens that reveal whether the reasoning was effective. By focusing on reflective tokens and discounting spurious certainty from appended reference text, R3 avoids two common pitfalls of log-prob aggregation. 

The reported results show consistent gains over ROUGE and aggregate-certainty baselines on ParaRev, and parity or better than binary correctness at higher Pass@k on FinQA. If validated more broadly, DRO with R3 could become a standard post-training option for writing, summarization, and analysis tasks that lack clean verifiers. 

Readers interested in reproducing the ParaRev setup should review the dataset and context augmentation details, and teams with math or code tasks might explore R3 as a complement to traditional verifiable rewards.

​

Definitions

RLVR. Reinforcement Learning with Verifiable Rewards. A training setup where the model’s output can be automatically checked for correctness (e.g., test pass/fail, numeric equivalence), removing the need for a learned reward model.

GRPO. Group Relative Policy Optimization. A PPO-style method that normalizes rewards across a group of sampled trajectories for the same prompt to stabilize advantage estimates (Shao et al., 2024).

Chain-of-Thought (CoT). A multi-step, natural language rationale produced by an LLM that conditions and explains the final answer (Wei et al., 2022).

R3 (Reasoning Reflection Reward). A token-level reward that weights reference tokens by how sensitive their likelihoods are to changes in the model’s chain-of-thought and corrects for certainty that arises from previously appended reference tokens.

ParaRev. A dataset for scientific paragraph revision with revision instructions and reviewer comments (Jourdan et al., 2025).

FinQA. A dataset for numerical reasoning over financial documents with expert-authored questions, programs, and answers (Chen et al., 2021).

References

(Xu et al., 2025) Direct Reasoning Optimization: LLMs Can Reward And Refine Their Own Reasoning for Open-Ended Tasks.

(Chen et al., 2021) FinQA: A Dataset of Numerical Reasoning over Financial Data.

(Jourdan et al., 2025) ParaRev: Building a dataset for Scientific Paragraph Revision annotated with revision instruction.

(Jourdan et al., 2024) CASIMIR: A corpus of scientific articles with integrated revisions.

(Shao et al., 2024) DeepSeekMath: Pushing the limits of mathematical reasoning in open models (introduces GRPO).

(Wei et al., 2022) Chain-of-thought prompting elicits reasoning in LLMs.

(Zheng et al., 2023) Judging LLM-as-a-judge with MT-Bench and Chatbot Arena.

(Gu et al., 2024) A survey on LLM-as-a-judge.