AlphaEvolve: AI-Powered Mathematical Discovery at Scale

Key Takeaways

• AlphaEvolve successfully tackled 67 mathematical problems, rediscovering best-known solutions in most cases and discovering improvements in several, with setup times of just a few hours per problem compared to months or years of traditional mathematical work.
  
  
• The system operates in two primary modes: a search mode that evolves heuristic algorithms to find optimal constructions, and a generalizer mode that discovers formulas valid across all input values from patterns in finite examples.
  
  
• When combined with Deep Think and AlphaProof, AlphaEvolve achieved complete automation from discovery to formal proof verification, exemplified by the finite field Kakeya problem where it discovered constructions, generated proofs, and formalized them in Lean.
  
  
• The approach demonstrates that LLM-guided evolutionary search excels at discovering constructions within reach of current mathematics but requires genuinely new deep insights for problems that resist standard combinatorial techniques.
  
  
• Critical to success are well-designed evaluation functions, continuous rather than discrete loss functions, expert domain knowledge in prompting, and training across families of related problems rather than isolated instances.

Evolutionary Computation Meets Mathematical Insight

At its foundation, AlphaEvolve implements a sophisticated evolutionary framework that maintains a population of computer programs, each encoding a potential solution or search strategy for a given mathematical problem. 

The system iteratively improves this population through natural selection (evolutionary) principles where a large language model serves as the generator, introducing intelligent mutations to high-performing programs rather than random character changes, while an evaluator, typically user-provided code, assigns fitness scores based on how well each program performs its designated task.

The crucial innovation lies in what AlphaEvolve evolves. Rather than directly generating mathematical objects like graphs or geometric configurations, the system operates in search mode, evolving programs that search for such objects. 

Each evolved program acts as a heuristic search algorithm, given a fixed time budget (typically 100 seconds) to find the best possible construction. This meta-level evolution, optimizing the optimization process itself, resolves a fundamental speed disparity that while LLM calls are expensive, they trigger massive cheap computations where evolved heuristics can explore millions of candidate constructions.

The system doesn't start from scratch each iteration; instead, new heuristics are evaluated on their ability to improve the best construction found so far, creating specialized early-stage heuristics for broad exploration and later-stage heuristics for fine-tuning near-optimal configurations. This dynamic adaptation attempts to mirror how human mathematicians approach problems differently at different stages of investigation.

The generalizer mode represents an even more ambitious capability. Here, AlphaEvolve attempts to write programs that solve problems for any input size $n$ by evaluating performance across ranges of values. By observing its own optimal solutions for small $n$, the system spots patterns and generalizes them into constructions valid for all $n$. 

This mode produced some of the work's most exciting results, including a construction for the Nikodym problem that inspired a new paper by Terence Tao (A Nikodym set construction over finite fields, in preparation), and discoveries in the finite field Kakeya problem that were automatically proven correct by Deep Think and formalized in Lean by AlphaProof demonstrating a complete AI-assisted mathematical pipeline from pattern recognition through rigorous formal verification.

Why This Breakthrough Matters

AlphaEvolve fundamentally changes the economics and accessibility of mathematical discovery. Traditional computational approaches to extremal problems require expert mathematicians to spend weeks or months crafting specialized algorithms, heuristics, and search strategies for each new problem. 

The expertise barrier is high, the iteration cycles are slow, and scaling across dozens of related problems becomes prohibitively expensive in human time. AlphaEvolve inverts this mode by using a clear problem specification, evaluation function, and a few hours of setup, the system can systematically explore mathematical spaces that would take human experts significantly longer to navigate. 

This process helps to democratize mathematical computation by allowing mathematicians to pose questions and receive sophisticated computational assistance without becoming programming experts themselves.

The ability to pipeline multiple AI systems represents a profound methodological advance. When AlphaEvolve discovered an interesting construction for the finite field Kakeya problem, Deep Think derived a proof of its correctness and a closed-form formula for its size, which AlphaProof then formally verified in Lean. 

This workflow of combining pattern discovery, symbolic proof generation, and formal verification, suggests future scenarios where mathematical conjectures could be semi-automatically explored, tested, proven, and validated with minimal human intervention. Such integration doesn't diminish the role of human mathematicians; rather, it shifts their focus from computational grunt work toward higher-level conceptual insights, conjecture formation, and interpretation of AI-generated results.

Perhaps most importantly, AlphaEvolve provides a new diagnostic tool for mathematical difficulty. The authors propose that future work could classify mathematical problems as "AlphaEvolve-hard" versus amenable to evolutionary approaches, creating a computational complexity hierarchy for mathematical existence proofs. 

Problems where AlphaEvolve succeeds typically involve clever combinations of known techniques rather than fundamentally new theoretical insights, while resistant problems may signal the need for breakthrough conceptual advances. This classification helps direct research efforts by knowing whether a problem is likely to yield to computational methods versus requiring deep theoretical work that informs resource allocation and research strategy across the mathematical community.

Empirical Results and Technical Insights

Across 67 problems spanning diverse mathematical domains, AlphaEvolve demonstrated remarkable versatility. In autocorrelation inequalities, the system not only matched literature bounds but revealed interesting trade-offs between computational resources and discovery speed. 

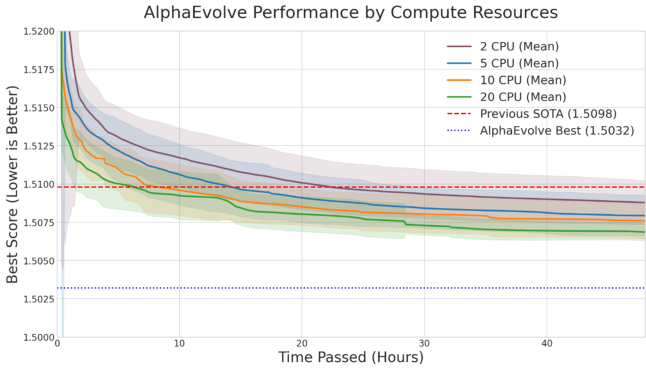
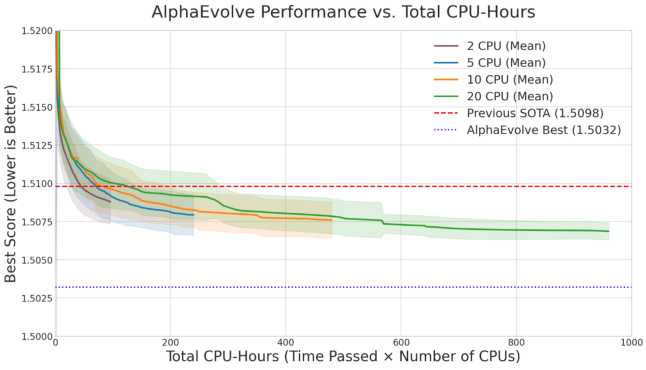
Image Credit: Tao et al.

Using 20 parallel CPU threads rather than 2 accelerated discovery significantly but approximately doubled total LLM queries, illustrating the cost-speed tension in evolutionary search. For difference bases, kissing numbers, and sphere packing problems, AlphaEvolve consistently approached or matched known optimal solutions, often discovering elegant programmatic descriptions that human mathematicians could study and extend.

The meta-analyses revealed surprising insights about model selection and resource allocation. Comparing high-end versus economical LLMs on simple problems like autocorrelation inequalities showed that while powerful models generated higher-quality suggestions faster, the most cost-effective strategy for basic optimization often involved running many experiments with cheaper models to maximize diversity. 

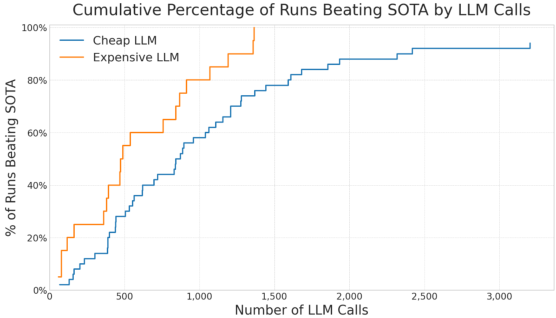
Image Credit: Tao et al.

For a few dollars in total LLM costs, researchers could match the performance of expensive models on straightforward problems. However, for complex challenges like Nikodym sets requiring elaborate constructions, only state-of-the-art LLMs succeeded in generating sufficiently sophisticated code. This nuanced picture suggests hybrid strategies should use economical models for broad exploration and expensive models for problems requiring deep mathematical structure.

Critical design choices emerged from the experiments. Verifier design proved essential, poorly constructed scoring functions led AlphaEvolve toward trivial or degenerate solutions, while well-designed verifiers incorporating domain knowledge guided the search effectively. Effectively lowering the barrier to discovery but not completely removing it since domain expertise in prompting is essential for on desired evolution.

Continuous loss functions consistently outperformed discrete ones, as seen in Problem 6.54 involving touching cylinders where distance-based continuous scoring enabled much faster convergence than binary legal-illegal categorization. The phenomenon of "cheating"—where the system exploited loopholes in problem formulations rather than finding genuine solutions—highlighted the importance of robust evaluation environments. When constraints like positivity were approximated discretely rather than enforced globally, AlphaEvolve sometimes found technically valid but mathematically meaningless solutions.

Expert prompting made substantial differences. Users with deep domain expertise consistently achieved better results than non-experts, confirming that AlphaEvolve functions best as a human-AI collaboration tool rather than a fully autonomous system. Providing insightful mathematical advice in prompts such as suggesting relevant techniques, known partial results, or structural properties - allowed AlphaEvolve to focus its evolutionary search more effectively. 

Interestingly, constraining the system to work with less data sometimes improved generalization in the generalizer mode, as forcing the system to learn patterns from small $n$ values encouraged discovery of more fundamental principles rather than overfitting to large datasets.

Training across families of related problems proved highly effective. When tackling geometric problems with varying point counts $n$ and dimensions $d$ simultaneously, search heuristics that performed well for one $(n,d)$ pair often provided strong foundations for others, guiding the system toward more universal principles. 

This cross-problem learning represents a form of meta-learning where evolutionary strategies themselves become transferable knowledge, dramatically reducing the computational cost of exploring related mathematical trajectories.

Looking Forward in Computational Mathematics

AlphaEvolve marks a significant milestone in AI-assisted mathematics, demonstrating that large language models can complement human intuition in discovering explicit constructions for longstanding mathematical problems. 

The system's ability to operate at scale—systematically exploring dozens of problems with minimal per-problem setup—distinguishes it from traditional computational approaches that require extensive customization for each new challenge. 

While AlphaEvolve excels at problems amenable to optimization and clever recombination of known techniques, it appropriately stops short of claiming general-purpose mathematical problem-solving, acknowledging that problems requiring fundamentally new theoretical insights remain outside its current scope.

The integration with Deep Think and AlphaProof points toward a powerful future methodology where discovery, proof generation, and formal verification form an integrated workflow. As these systems mature and their integration deepens, the boundary between computational exploration and rigorous proof may blur productively. 

Mathematicians could pose conjectures, receive AI-generated constructions and proofs, then focus their expertise on interpretation, generalization, and understanding rather than computational verification. This division of labor plays to the strengths of both human and artificial intelligence.

For researchers interested in applying these techniques to their domains, the AlphaEvolve team has released a live repository of problems with experimental code and extended details, enabling reproduction and extension of their work despite the inherent randomness in evolutionary processes. 

The authors suggest several promising directions: enabling AlphaEvolve to select its own hyperparameters dynamically, expanding the range of problems it can address, and developing better frameworks for incorporating computer-assisted proofs automatically into the system's output. 

As mathematical communities explore these tools, we can expect new classifications of problem difficulty, novel human-AI collaboration patterns, and accelerated progress on construction-oriented mathematical challenges across pure and applied domains.

The paper demonstrates that the intersection of large language models and evolutionary computation creates powerful new capabilities for mathematical exploration. By searching in the space of programs rather than solutions, AlphaEvolve discovers not just what mathematical objects exist but how to construct them—generating interpretable artifacts that advance human understanding alongside computational discovery. 

This represents not the replacement of human mathematicians but a significant augmentation of their capabilities, offering new pathways to tackle problems at the frontiers of combinatorics, analysis, and geometry.

google-deepmind

Organization

alphaevolve_repository_of_problems

55

1

0

Apache License 2.0

11.6k KB

1 Network

1 Subscribers

Jupyter Notebook

Definitions

Evolutionary Computation

A family of algorithms inspired by biological evolution that maintain populations of candidate solutions, using selection, mutation, and crossover to iteratively improve solution quality over generations.

Large Language Model (LLM)

A type of artificial neural network trained on vast text corpora to predict and generate human-like text, capable of understanding context and generating code or natural language based on prompts.

FunSearch

DeepMind's predecessor system to AlphaEvolve that evolved Python functions (typically 10-20 lines) to solve mathematical and optimization problems, demonstrating the feasibility of LLM-guided program search.

Finite Field Kakeya Problem

A problem in combinatorial geometry asking for the minimum size of a set in a finite field vector space that contains a line in every direction, with connections to harmonic analysis and theoretical computer science.

Nikodym Problem

A geometric problem concerning sets that contain lines in many directions, related to questions about measure, dimension, and the structure of sets with special directional properties.

Extremal Combinatorics

A branch of combinatorics studying maximum or minimum sizes of combinatorial structures satisfying certain properties, such as the largest graph avoiding specific substructures.

Autocorrelation Inequality

A mathematical inequality relating a function to shifted versions of itself, important in harmonic analysis, signal processing, and various areas of pure mathematics.

Meta-level Evolution

The process of evolving not just solutions but the algorithms that find solutions, creating a recursive optimization where search strategies themselves become the objects of evolutionary improvement.

Deep Think

An AI system developed by DeepMind capable of extended mathematical reasoning, proof generation, and symbolic manipulation, which achieved gold-medal performance at the 2025 International Mathematical Olympiad.

AlphaProof

DeepMind's formal verification system that can generate and verify mathematical proofs in the Lean proof assistant, enabling automated checking of mathematical correctness with the highest rigor standards.

Lean

A formal proof assistant and programming language that allows mathematical theorems to be stated and proven with computer-verified correctness, eliminating the possibility of logical errors in complex arguments.

Kolmogorov Complexity

A measure of the computational resources needed to specify an object, defined as the length of the shortest computer program that produces the object as output.