UC Berkley Research How Coin Flips Help LLMs Think Like Bayesian Statisticians

This research from UC Berkley investigates whether large language models (LLMs) utilize in-context learning (ICL) to perform structured reasoning consistent with Bayesian inference or rely on pattern matching.

https://arxiv.org/html/2503.04722v1

Key Takeaways

• LLMs often possess biased priors, leading to initial divergence in zero-shot settings.
• In-context evidence outweighs explicit bias instructions.
• ICL (In Context Learning) can correct mis-calibrated priors in a straightforward setting
  
• LLMs broadly follow Bayesian posterior updates, with deviations primarily due to mis-calibrated priors rather than flawed updates.
• Attention magnitude has negligible effect on Bayesian inference.

Overview

Large language models (LLMs) have demonstrated remarkable capabilities in tasks beyond simple language prediction, notably through in-context learning (ICL), where models generalize from few-shot examples provided in their input prompts. This emergent ability allows LLMs to adapt to new tasks without explicit retraining.

The study explores whether LLMs' ICL mechanisms align with Bayesian reasoning—a statistical framework where prior beliefs are updated with new evidence to form previous beliefs. Understanding this alignment is crucial, as it sheds light on whether LLMs perform structured reasoning or merely replicate patterns from training data.

To investigate this, the researchers employed a controlled experimental setup involving biased coin flips. This scenario allows for precise calculation of Bayesian quantities, facilitating a clear assessment of LLMs' inferential behaviors. By examining how LLMs estimate coin biases and incorporate sequential evidence, the study assesses the degree to which these models adhere to normative probabilistic reasoning.

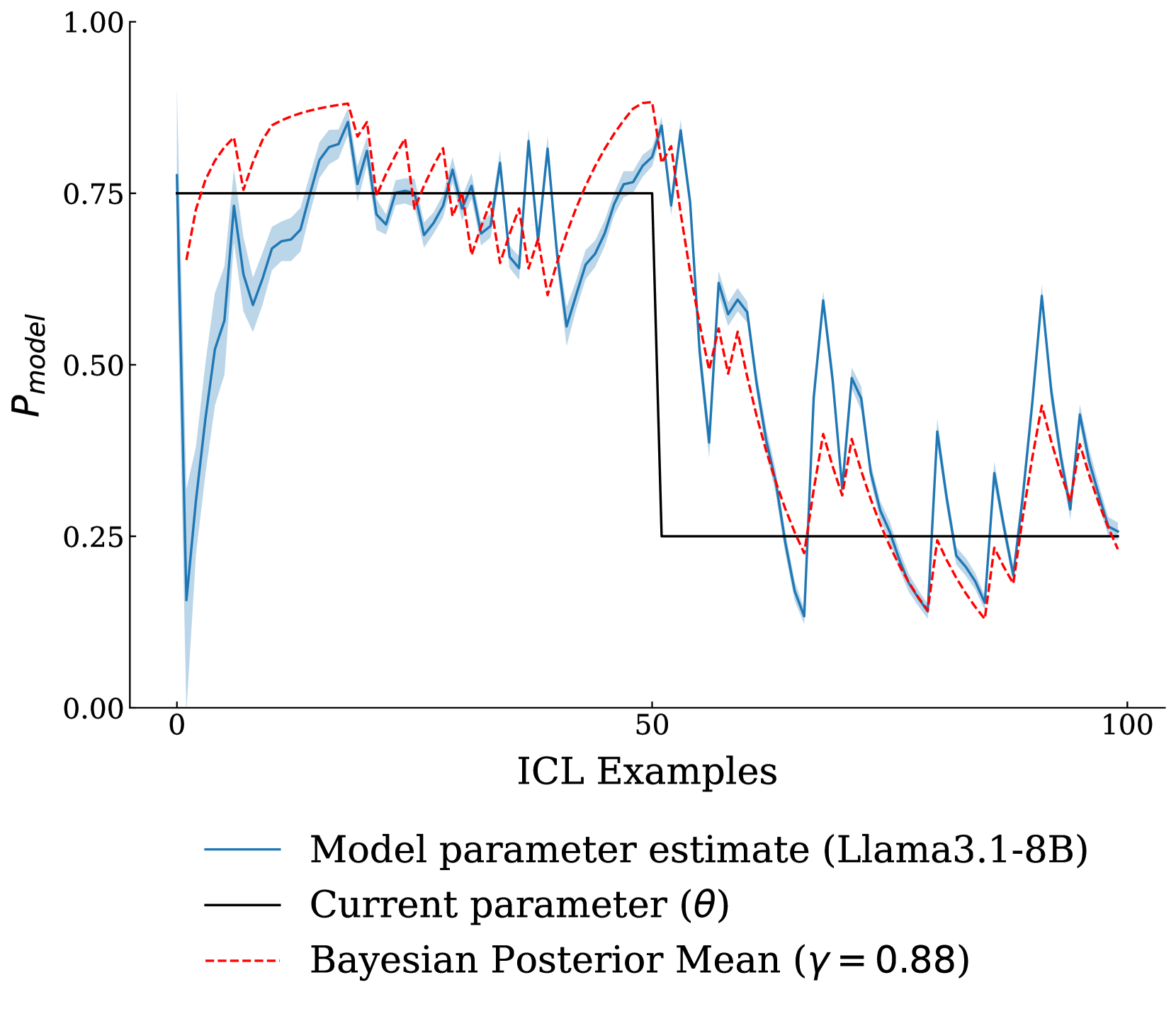
Figure 1:When we ask large language models (LLMs) to model sequences with in-context learning (ICL), how do they adapt their posterior probabilities given the provided examples? This figure explores how model probabilities change as we add new ICL examples in a biased coin-flipping experiment. The X-axis represents steps in the trajectory, while the Y-axis shows the predicted parameter of a Bernoulli distribution. Our results reveal that, while LLMs often have poorly calibrated priors, their updated parameter estimates broadly align with Bayesian behavior.

Why It's Important

The findings of this research have implications for the use of LLMs in various domains. In complex environments for example in robotics simulations or human behavior modeling, accurate simulation relies heavily on well-calibrated base assumptions. 

The study underscores that, without calibration or sufficient prompting, LLMs may misrepresent even simple coin-flip dynamics. However, once given an adequate stream of observations, these models exhibit behavior that aligns well with normative Bayesian reasoning.

This work highlights how ICL (In Context Learning) can correct mis-calibrated priors in a straightforward setting. In more complex scenarios, additional strategies—such as explicit prior calibration or dynamic tuning of prompt design—may be necessary to ensure reliable probabilistic modeling. 

By grounding the analysis in a simple and interpretable domain, the research provides a foundation for further refining the "LLM-as-world-model" framework and deepening the understanding of how LLMs handle uncertainty in realistic, evolving environments.

Understanding whether LLMs perform Bayesian-like updates has significant implications for their application across various domains:

• Model Calibration: If LLMs can adjust their priors based on new evidence, they can be better calibrated for tasks requiring probabilistic reasoning, enhancing their reliability.
  
  

• Decision Making: In fields like healthcare or finance, where decisions are made under uncertainty, LLMs capable of Bayesian reasoning can provide more nuanced and trustworthy insights.
  
  

• AI Alignment: Aligning AI behavior with human reasoning patterns is crucial for trust and safety. Demonstrating Bayesian reasoning in LLMs brings them closer to human-like inferential processes.

Experimental Setup

The researchers used a scenario involving biased coin flips as their experimental framework. Each experimental trial provided a series of coin flips with controlled biases, allowing the researchers to precisely compute the Bayesian posterior distribution. 

This setup enabled a direct comparison between the LLMs' predictive behaviors and the theoretical Bayesian inference outcomes. The experiments varied in the length of evidence sequences, coin biases, and the explicit instructions provided to the models. 

By analyzing the models' outputs across these conditions, the study evaluated how effectively LLMs integrate prior beliefs with new evidence in a probabilistic context.

Limitations

While the study demonstrates that LLMs can approximate Bayesian inference through in-context learning, several limitations merit consideration:

1. Evaluation Scope: The methodology captures only a limited portion of the full posterior distribution. Specifically, it evaluates the model's explicit token probabilities for predefined completions, potentially overlooking alternative valid outcomes. For example, if the expected response is "The coin came up 'heads'," the model might alternatively generate "The coin landed on the edge of heads" or "The coin was slightly tilted toward heads." While these are low-probability outcomes, they represent probability mass not incorporated into the evaluation, possibly misrepresenting the model's Bayesian updating accuracy. 
   
   

2. Simplified Experimental Setup: The experiments focus on discrete, categorical predictions (e.g., biased coin flips), which may not fully capture the complexities of real-world probabilistic reasoning. Bayesian inference in natural settings often involves continuous distributions, hierarchical priors, or distributions with long tails. Therefore, findings from this simplified setup may not generalize to more complex probabilistic environments where likelihoods are less structured or where prior distributions must be inferred over high-dimensional latent spaces.
   
   

3. Closed-Source Model Evaluation: The approach relies on extracting logits to approximate posterior distributions, limiting its applicability to open-source models. Evaluating closed-source models, such as GPT-4 or Claude, poses challenges due to inaccessible internals. While alternative methods, like sampling via API calls, could approximate the posterior, they are costly and susceptible to distortions from API-side interventions (e.g., caching, response smoothing, temperature adjustments), potentially introducing artifacts that obscure the model's true Bayesian reasoning capabilities. 
   
   

4. Prior Calibration: LLMs often exhibit poorly calibrated priors during in-context learning, leading to systematic misestimation in early predictions. While models update their beliefs in a manner consistent with Bayesian inference, inaccurate priors can cause significant initial divergence from the true posterior. This misalignment is particularly concerning in high-stakes applications, such as financial forecasting or scientific modeling, where incorrect priors can propagate errors through downstream reasoning. 

These limitations underscore the need for further research to enhance LLMs' probabilistic reasoning capabilities, particularly in complex, real-world scenarios.

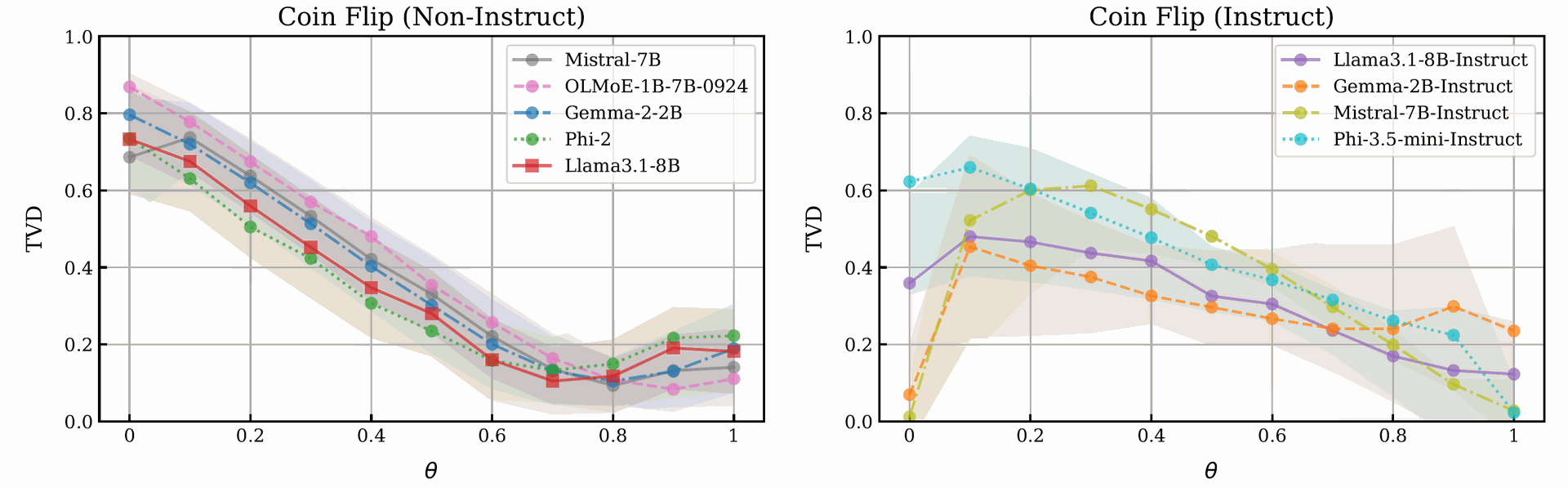
Figure 3: Biased coins: Plots of mean total variation distance (TVD, ↓) against bias (θ) for non-instruct (left) and instruct (right) models when aggregated across prompts (N=50) for the biased coin flip experiment. Shaded areas show one standard deviation. While non-instruct models both (1) ignore biasing instructions in the prompts and (2) almost always generate a biased distribution (≈70% heads), instruct-based models pay better attention to biasing

information, and perform significantly better when modeling extreme bias (always generating heads/tails).

Summary of Results

The study found that language models often exhibit biased priors for stochastic phenomena, leading to significant initial divergence when modeling zero-shot scenarios. They tend to disregard explicit bias instructions and rely more heavily on in-context examples. Their predictions are consistent with Bayesian updates once new evidence is presented, with most deviations from the true posterior arising from mis-calibrated priors rather than faulty updates. Attention magnitude has minimal influence on the updating process.

The experiments revealed that models converge to the expected distribution as more evidence is provided via in-context learning. Larger models do not necessarily perform better at incorporating in-context-based evidence. The study also found that models implicitly apply a localized Bayesian update with a shorter time horizon, aligning better with a slightly discounted filtering process.

The study's experiments yielded several key findings:

1. Biased Priors in LLMs: LLMs often exhibit inherent biases in their prior distributions, leading to significant initial divergence when modeling zero-shot scenarios. For instance, models displayed a bias towards predicting 'heads' in coin flip scenarios, even when the true distribution was balanced.
   
   

2. In-Context Evidence vs. Explicit Instructions: LLMs tend to rely more heavily on in-context examples than explicit bias instructions. When provided with sequences of biased coin flips, models adjusted their predictions accordingly, even if explicit instructions suggested a different bias.
   
   

3. Bayesian Posterior Updates: Upon receiving in-context evidence, LLMs' predictions aligned with Bayesian updates. Deviations from the true posterior were primarily due to miscalibrated priors rather than flaws in the updating mechanism. This suggests that while LLMs can perform Bayesian-like updates, the accuracy of their inferences depends on the calibration of their initial beliefs.
   
   

4. Attention Magnitude's Negligible Impact: The magnitude of attention weights assigned to in-context examples had minimal influence on the models' Bayesian inference capabilities. This indicates that other factors, such as the quality and quantity of in-context data, play more critical roles in guiding LLMs' inferential processes.

Conclusion

The research provides evidence that LLMs, through in-context learning, can perform reasoning processes akin to Bayesian inference. However, the presence of biased priors highlights the need for careful calibration to ensure accurate probabilistic reasoning. These insights deepen our understanding of LLMs' inferential mechanisms and inform their application in domains requiring structured reasoning under uncertainty.