Recent advancements in Large Language Models (LLMs) have led to the development of specialized variants known as Large Reasoning Models (LRMs), which incorporate mechanisms like Chain-of-Thought (CoT) to generate detailed thinking processes alongside answers.
While these models have shown improved results on reasoning tasks, their core capabilities, scaling properties, and limitations remain not fully understood. Traditional evaluation methods, often relying on established mathematical and coding benchmarks, can suffer from issues like data contamination and don't offer insights into the internal reasoning process.
This research investigates these gaps by systematically examining frontier LRMs using controllable puzzle environments that allow for precise manipulation of complexity while maintaining consistent logical structures. By analyzing both final answers and the internal reasoning traces ("thoughts"), the study aims to shed light on how LRMs "think" and reveal their strengths and fundamental limitations.
Key Takeaways
- Accuracy Collapse: Frontier LRMs experience a complete accuracy collapse beyond certain problem complexities.
- Counter-intuitive Reasoning Effort: As problems approach the point of accuracy collapse, LRMs counter-intuitively reduce their reasoning effort (measured in thinking tokens) despite increasing problem difficulty and having ample token budget. This suggests a fundamental scaling limitation.
- Three Performance Regimes: Comparing LRMs with standard LLMs under equivalent compute reveals three distinct performance regimes based on complexity: at low complexity, standard models are often more accurate and efficient; at medium complexity, LRMs with additional thinking show an advantage; and at high complexity, both model types fail.
- Limitations in Exact Computation: LRMs demonstrate limitations in executing exact computations and following logical steps. Providing an explicit algorithm for a puzzle did not improve performance or prevent collapse.
- Inconsistent Reasoning: LRMs reason inconsistently across different types of puzzles, showing vastly different error patterns even for problems requiring a similar number of steps.
- Complexity-Dependent Thinking Patterns: Analysis of reasoning traces shows different patterns based on complexity: "overthinking" (finding the correct solution early but continuing to explore incorrect paths) at low complexity, finding correct solutions later in the thought process at medium complexity, and complete failure to find correct solutions at high complexity.
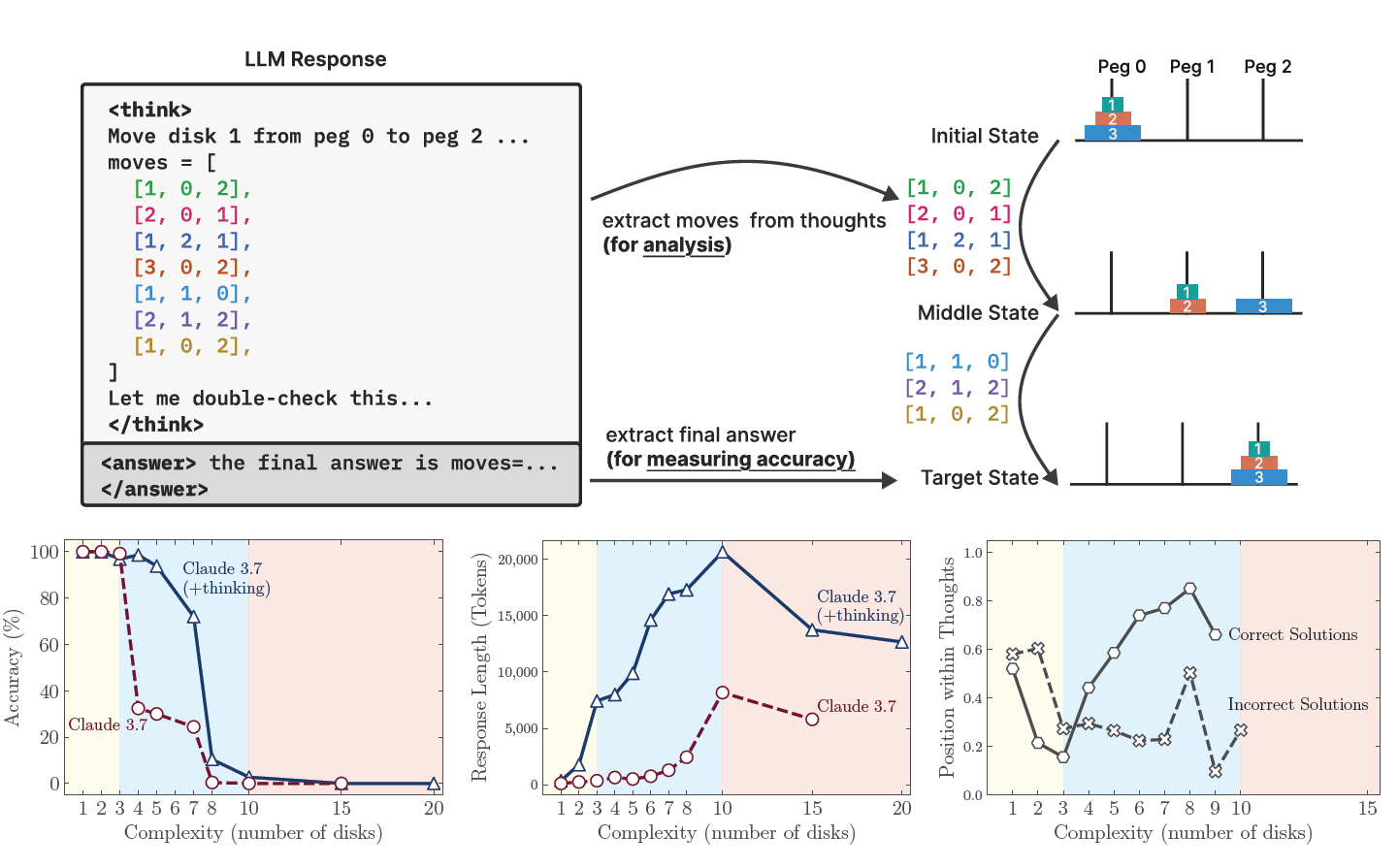
Figure 1: Top: Our setup enables verification of both final answers and intermediate reasoning traces, allowing detailed analysis of model thinking behavior. Bottom left & middle: At low complexity, non-thinking models are more accurate and token-efficient. As complexity increases, reasoning models outperform but require more tokens—until both collapse beyond a critical threshold, with shorter traces. Bottom right: For correctly solved cases, Claude 3.7 Thinking tends to find answers early at low complexity and later at higher complexity. In failed cases, it often fixates on an early wrong answer, wasting the remaining token budget. Both cases reveal inefficiencies in the reasoning process.
Overview
Large Language Models (LLMs) have evolved significantly, with recent generations including specialized variants designed for complex reasoning tasks. These are referred to as Large Reasoning Models (LRMs), and examples include OpenAI's o1/o3, DeepSeek-R1, Claude 3.7 Sonnet Thinking, and Gemini Thinking.
A key characteristic of LRMs is their use of "thinking" mechanisms, such as generating a Chain-of-Thought (CoT), which is a sequence of intermediate reasoning steps leading to a final answer.
While techniques like CoT and self-verification have improved performance on reasoning benchmarks, obtaining high-quality data for training these thinking processes can be expensive and difficult to acquire. To address this limitation some models, like Deepseek-R1, have used reinforcement learning (RL) to enhance their thinking abilities.
Despite promising results on benchmarks, the fundamental benefits and limitations of LRMs remain unclear. Evaluating these models rigorously is challenging with existing benchmarks, primarily focused on mathematics and coding.
These benchmarks often suffer from data contamination, where models may have seen similar problems during training, making it difficult to assess true reasoning capabilities rather than memorization or pattern matching. Additionally, these benchmarks typically only evaluate the final answer, providing limited insight into the quality and structure of the reasoning process itself.
To address these limitations, researchers at Apple adopt a different evaluation paradigm using controllable puzzle environments.
These environments allow researchers to precisely control problem complexity by adjusting specific elements while keeping the underlying logical structure consistent. This setup avoids data contamination common in established benchmarks and emphasizes algorithmic reasoning, requiring models to follow explicit rules.
Crucially, these puzzles support simulator-based evaluation, enabling rigorous checking of each step in a solution and detailed analysis of failures. The study evaluated several frontier LRMs and their non-thinking counterparts, including Claude 3.7 Sonnet (with and without thinking) and DeepSeek (R1 and V3).
The experiments involved generating multiple samples for each puzzle instance at varying complexity levels and analyzing both the final answer accuracy and the intermediate "thinking tokens" using a custom extraction and validation pipeline.
Why it’s Important
The emergence of LRMs has been suggested as a potential shift in how LLM systems approach complex problem-solving, possibly representing steps towards more general artificial intelligence.
However, truly understanding whether these models possess generalizable reasoning abilities or are primarily relying on sophisticated pattern matching is a critical open question. This research moves beyond simply measuring benchmark performance to systematically investigate the fundamental capabilities and limitations of LRMs across increasing levels of problem difficulty.
By using controllable puzzle environments, the study provides a cleaner, more controlled way to probe reasoning behavior than potentially contaminated math or coding benchmarks.
The ability to analyze the intermediate reasoning traces allows for a deeper understanding of the models' problem-solving processes, revealing inefficiencies like "overthinking" and providing insights into self-correction mechanisms.
The findings on the accuracy collapse and the counter-intuitive reduction in reasoning effort at high complexities highlight a significant scaling limitation in current LRMs. This challenges the assumption that simply allocating more compute (via thinking tokens) will enable models to solve arbitrarily complex problems.
The observation that providing an explicit algorithm doesn't prevent collapse further suggests limitations in the models' ability to perform exact, step-by-step logical execution, which is crucial for robust reasoning and symbolic manipulation.
The inconsistency observed across different puzzle types, even for problems of similar required move counts, suggests that current LRMs may struggle with generalizing reasoning strategies across diverse logical structures or may be overly reliant on specific patterns encountered in training data for certain problem types.
These insights are vital for informing the design and deployment of future reasoning systems, indicating that simply scaling current approaches may not be sufficient to achieve truly generalizable reasoning capabilities.
The study's findings raise crucial questions for future research into the nature of reasoning in these models and the improvements needed to overcome these fundamental barriers.
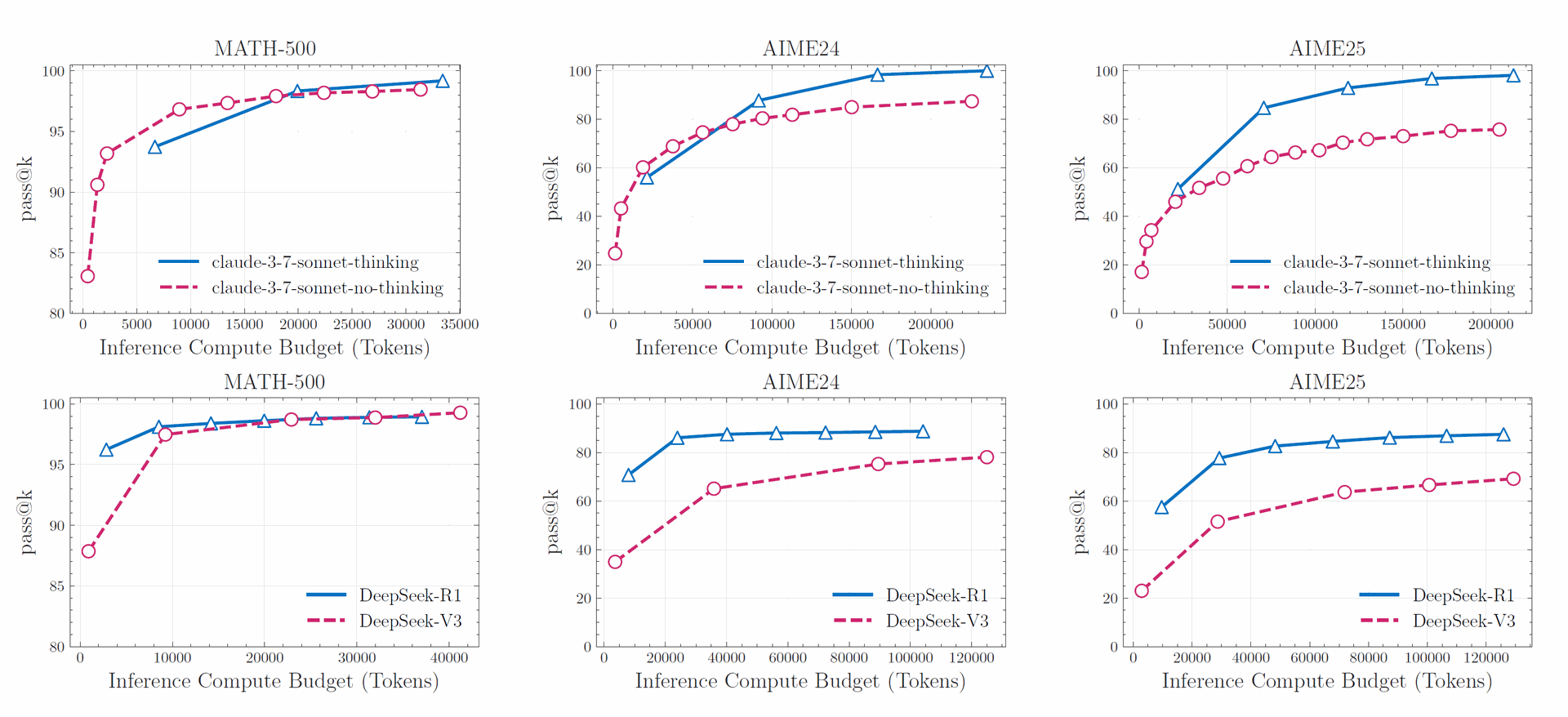
Figure 2: Comparative analysis of thinking versus non-thinking models across math benchmarks reveals inconsistent performance patterns. While results on the MATH-500 dataset show comparable performance between both model types, the thinking models demonstrate superior performance on AIME24 and AIME25 benchmarks. Additionally, the observed performance degradation from AIME24 to AIME25 highlights the vulnerability of these benchmarks to data contamination issues.
Summary of Results
The study conducted extensive experiments on frontier LRMs and their non-thinking counterparts using four controllable puzzle environments: Tower of Hanoi, Checker Jumping, River Crossing, and Blocks World.
These puzzles vary in their scaling of compositional depth (number of moves required) with problem size N. For example, Tower of Hanoi scales exponentially (2N - 1 moves), while Checker Jumping scales quadratically ((N+1)2 - 1 moves).
River Crossing and Blocks World show more near-linear growth in moves with N. The evaluation focused on solution correctness, verifiable step-by-step using puzzle simulators.
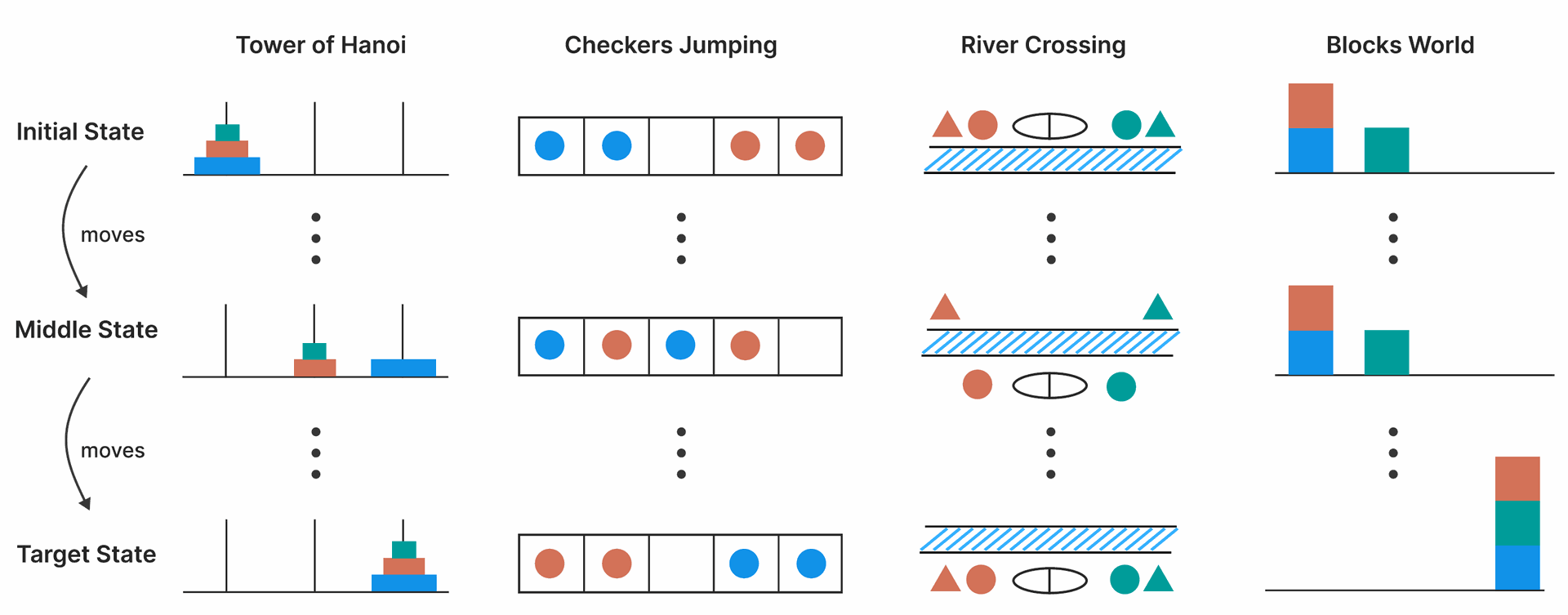
Figure 3: Illustration of the four puzzle environments. Columns show the progression from initial state (top) through intermediate state (middle) to target state (bottom) for puzzles: Tower of Hanoi (disk transfer across pegs), Checkers Jumping (position swapping of colored tokens), River Crossing (transporting entities across a river), and Blocks World (stack reconfiguration).
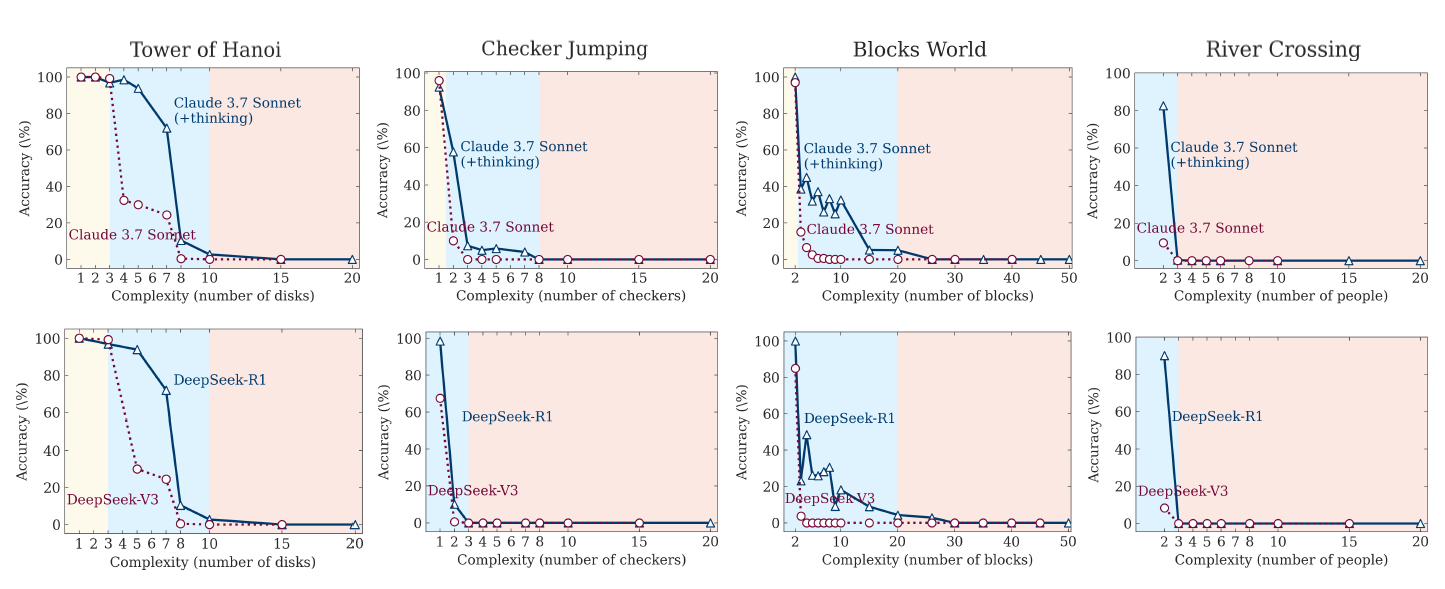
Figure 4: Accuracy of thinking models (Claude 3.7 Sonnet with thinking, DeepSeek-R1) versus their non-thinking counterparts (Claude 3.7 Sonnet, DeepSeek-V3) across all puzzle environments and varying levels of problem complexity.
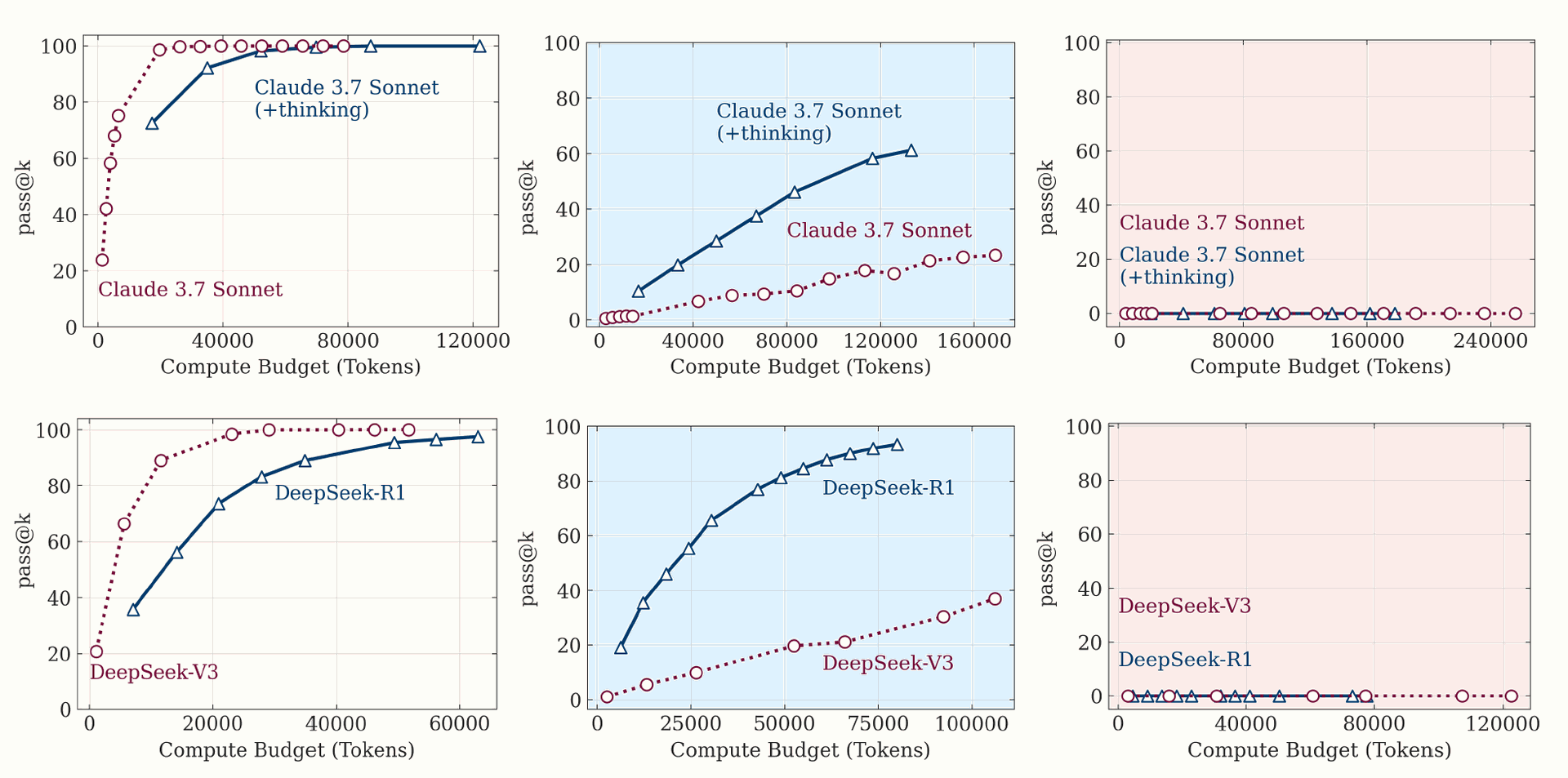
Figure 5: Pass@k performance of thinking vs. non-thinking models across equivalent compute budgets in puzzle environments of low , medium , and high complexity. Non-thinking models excel in simple problems, thinking models show advantages at medium complexity, while both approaches fail at high complexity regardless of compute allocation.
A key finding is the presence of three distinct performance regimes when comparing thinking and non-thinking models under equivalent inference compute.
- Low Complexity: For simpler problems, standard (non-thinking) LLMs often achieve comparable or even better accuracy than LRMs and are more token-efficient. Figure 4 and Figure 5 illustrate this, showing non-thinking models performing well at low N values.
- Medium Complexity: As complexity moderately increases, LRMs, capable of generating longer Chain-of-Thought, begin to show an advantage, and the performance gap widens. Figure 4 and Figure 5 visually depict this improvement for thinking models in the medium complexity range.
- High Complexity: When problems reach high complexity, the performance of both thinking and non-thinking models collapses completely to zero accuracy. Figure 4 and Figure 5 clearly show this collapse beyond a certain complexity threshold.
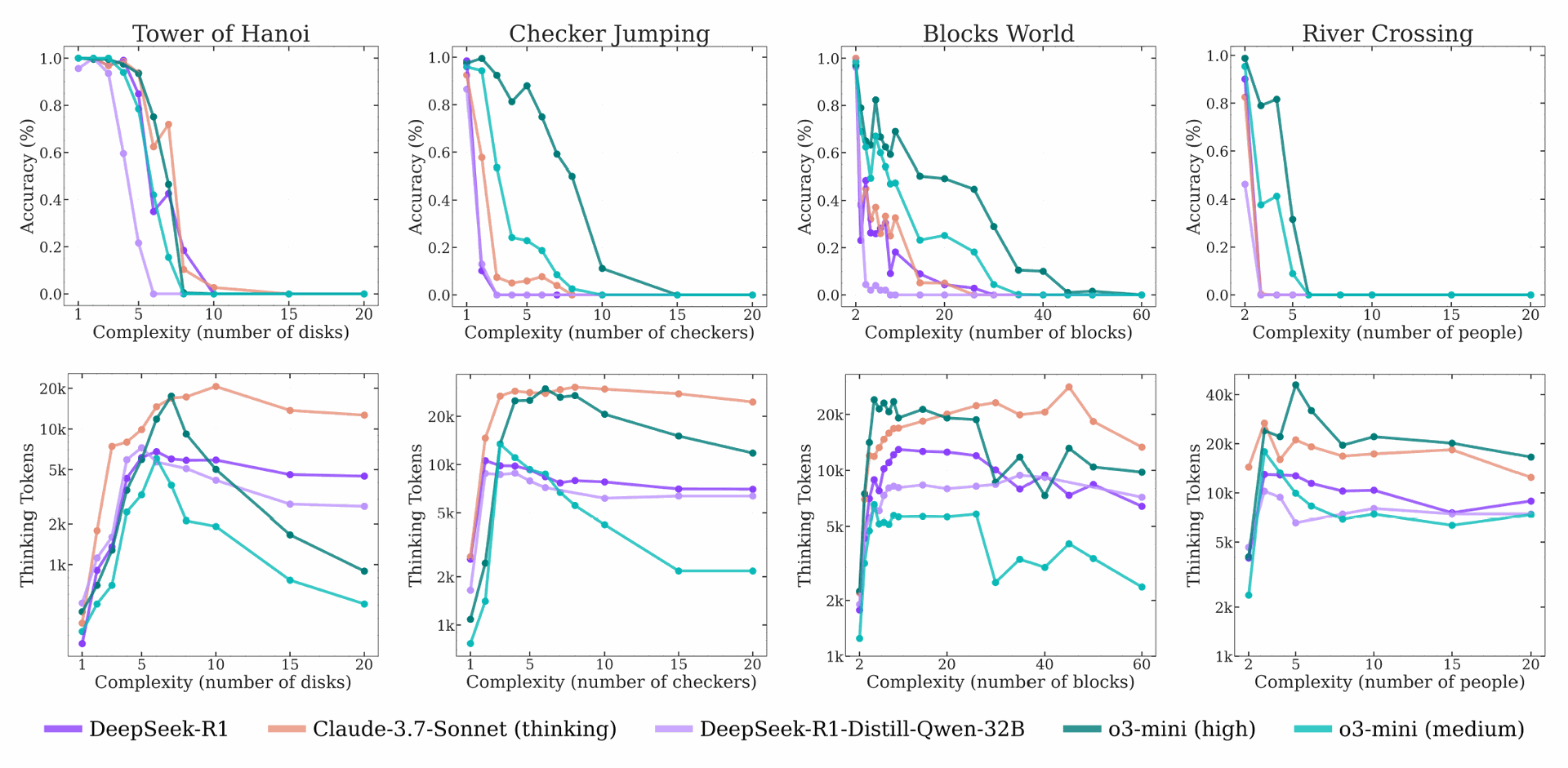
Figure 6: Accuracy and thinking tokens vs. problem complexity for reasoning models across puzzle environments. As complexity increases, reasoning models initially spend more tokens while accuracy declines gradually, until a critical point where reasoning collapses—performance drops sharply and reasoning effort decreases.
The study further analyzed the behavior of several state-of-the-art thinking models (o3-mini, DeepSeek-R1, DeepSeek-R1-Qwen-32B, and Claude-3.7-Sonnet thinking) as complexity increased. Figure 6 demonstrates that for all tested LRMs, accuracy declines as complexity rises, eventually leading to a complete accuracy collapse.
Simultaneously, an analysis of thinking token usage revealed a counter-intuitive pattern. Thinking tokens, a proxy for reasoning effort, initially increase with problem complexity, but upon approaching the accuracy collapse point, models reduce their reasoning effort despite the problem becoming harder and having a sufficient token budget.
This is visible in the bottom graphs of Figure 6 and across models in Figure 13. This phenomenon suggests a fundamental limitation in how current LRMs scale their thinking with problem difficulty.
Detailed analysis of the intermediate steps or "thoughts" within the reasoning traces of Claude-3.7-Sonnet-Thinking provided further insights.
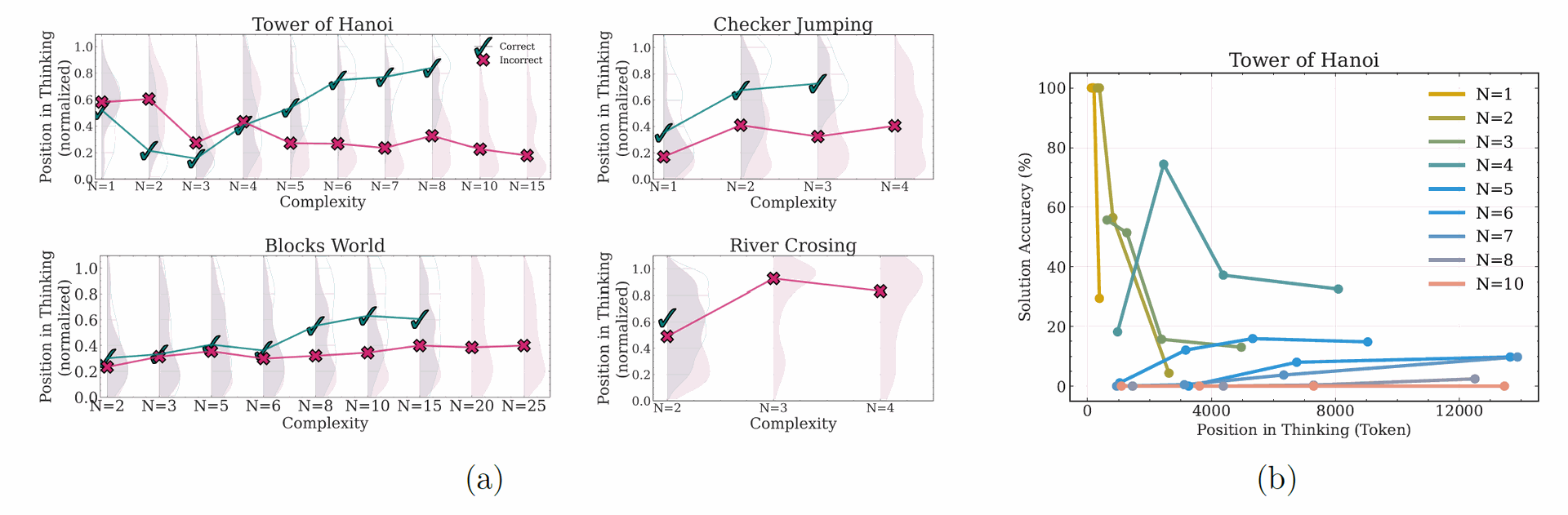
Figure 7: Left & Middle: Position and correctness of intermediate solutions within reasoning traces across four puzzles at varying complexity levels. ✓ indicates correct solutions, ✗ indicates incorrect solutions, with distribution density shown by shading; Right: Solution accuracy versus position in thinking for Tower of Hanoi at different complexity levels. Simple problems (N=1-3) show early accuracy declining over time (overthinking), moderate problems (N=4-7) show slight improvement in accuracy with continued reasoning, and complex problems (N≥8) exhibit consistently near-zero accuracy, indicating complete reasoning failure.
By extracting and validating intermediate solutions, the researchers identified complexity-dependent patterns. Figure 7a shows that for simple problems, correct solutions (green) tend to appear early, but the model continues exploring incorrect solutions (red) later in the thought process, illustrating the "overthinking phenomenon".
As complexity increases, correct solutions appear later in the reasoning trace after more exploration of incorrect paths. In the high-complexity "collapse mode," no correct solutions are found within the thoughts.
Figure 7b complements this, showing solution accuracy across sequential segments of thoughts; accuracy decreases/oscillates over time for simple problems, improves with thinking for moderate problems, and is zero for complex problems.
The study also uncovered surprising limitations in LRMs' ability to perform exact computation and maintain consistency.
In the Tower of Hanoi puzzle, even when the recursive algorithm was provided in the prompt, model performance did not significantly improve, and the accuracy collapse still occurred at similar complexities.
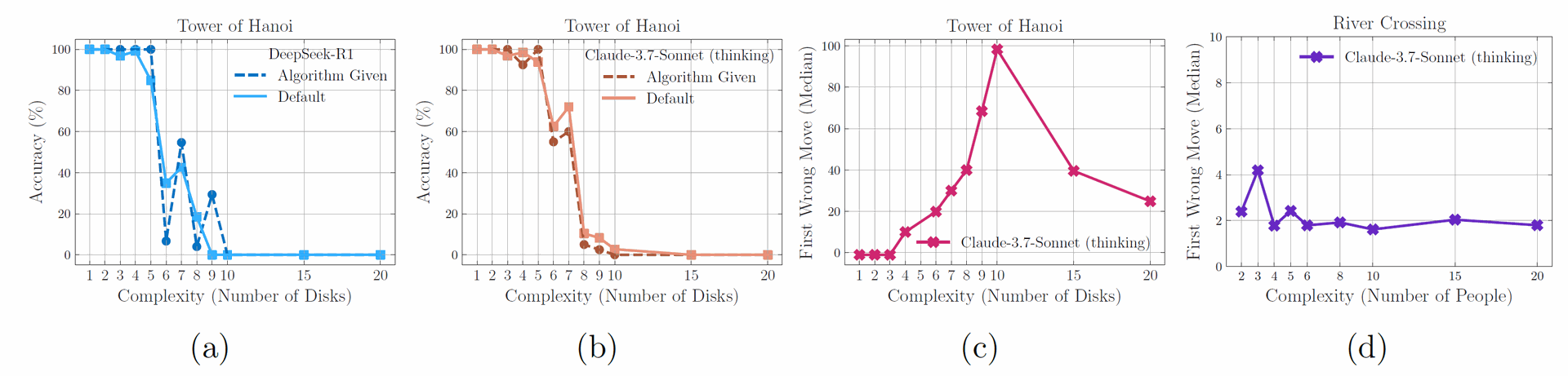
Figure 8: (a) & (b) Despite providing the solution algorithm in the prompt, execution failure occurs at similar points, highlighting reasoning model limitations in logical step execution. (c) & (d) Notably, the Claude 3.7 Sonnet model demonstrates much longer error-free sequences in the Tower of Hanoi compared to early errors in the River Crossing scenario.
Figure 8a and 8b show this lack of improvement when the algorithm is given. This suggests that the limitation isn't solely in devising a solution strategy but also in executing the logical steps accurately.
The Claude 3.7 Sonnet thinking model exhibited vastly different failure patterns across puzzles. It could produce long sequences of correct moves (median around 100 moves for N=10) in Tower of Hanoi but failed much earlier (median around 4 moves for N=3) in River Crossing, despite the latter requiring fewer total moves.
Figure 8c and 8d illustrate this inconsistency. This variability across puzzle types, even with similar computational complexity in terms of required moves, suggests potential issues with generalization or reliance on training data distribution.
Failure analysis examining the position of the first incorrect move showed that while thinking models, on average, fail later in a solution sequence than their non-thinking counterparts, their failure positions have higher variance, indicating less consistent performance.
Conclusion
This research systematically investigated the reasoning capabilities and limitations of frontier Large Reasoning Models (LRMs) using a controlled experimental approach with puzzle environments.
The findings highlight fundamental limitations, demonstrating that current LRMs fail to exhibit generalizable problem-solving abilities beyond specific complexity thresholds. The study identified three distinct performance regimes based on problem complexity: standard LLMs excel at low complexity, LRMs show an advantage at medium complexity, and both fail at high complexity.
A particularly striking finding is the counter-intuitive reduction in reasoning effort (thinking tokens) displayed by LRMs as they approach their accuracy collapse point. This suggests an inherent scaling limitation in their thinking process related to increasing problem difficulty.
The detailed analysis of reasoning traces revealed how the strategy changes with complexity, shifting from "overthinking" simpler problems to exploring incorrect paths before finding solutions at moderate complexities, and ultimately failing to find any correct steps at high complexities.
The study exposed surprising limitations, such as the failure of LRMs to leverage explicit algorithms to improve performance on complex problems and inconsistent reasoning behavior across different puzzle types.
These results challenge prevailing assumptions about the capabilities of current LRMs, suggesting they may be encountering fundamental barriers to achieving truly generalizable reasoning.
The findings raise critical open questions for future research, particularly concerning the models' symbolic manipulation capabilities, their ability to perform exact step-by-step computation, and the factors contributing to inconsistency across different problem structures. The insights provided by this controlled evaluation approach can inform the development of more robust and generalizable reasoning systems in the future. However, the authors acknowledge limitations, including the focus on a specific slice of reasoning tasks and the use of black-box access to models.

The Illusion of Thinking: Unpacking the Strengths and Striking Limitations of Large Reasoning Models
The Illusion of Thinking: Understanding the Strengths and Limitations of Reasoning Models via the Lens of Problem Complexity