Scientific optimization plays a crucial role across various domains, including mathematics, physics, and chemistry. Large Language Models (LLMs) have been increasingly used for mathematical optimization due to their reasoning capabilities.
However, existing prompt-based optimization approaches suffer from sensitivity to prompt structures and difficulties handling long observational feedback sequences. The authors propose a General Scientific Optimizer (GSO), a bi-level optimization framework integrating model editing techniques into LLMs to refine solutions iteratively.
Key Takeaways
- New Bi-Level Optimization Approach: GSO leverages LLMs as reasoning agents (outer-level optimization) and simulators as experimental platforms (inner-level optimization) to iteratively refine scientific solutions.
- Model Editing for Improved Optimization: GSO incorporates model editing to adjust LLMs dynamically using feedback from simulations, preventing performance degradation due to long input sequences.
- Outperforms Existing Methods: GSO consistently surpasses state-of-the-art methods such as Funsearch, Eureka, OPRO, and SGA across seven scientific optimization tasks.
- Broad Applicability: The framework is tested on diverse problems, including linear regression, the Traveling Salesman Problem (TSP), constitutive law prediction, and molecular property optimization.
- Robustness to Prompt Sensitivity: Unlike traditional prompt-based methods, GSO is less sensitive to prompt variations, reducing the need for manual prompt tuning.
Overview
Optimization is a fundamental process in scientific research, enabling advancements in various scientific domains, including mathematics, physics, chemistry, pharmacology, and more .
Despite the increasing use of LLMs in optimization, their efficiency is hampered by prompt sensitivity and challenges in processing long observational feedback. Existing methods rely on iterative prompt tuning, making them domain-specific, sensitive to input prompt variability and computationally expensive.
The authors introduce GSO (General Scientific Optimizer), a generalized framework that integrates LLMs and simulations into a structured bi-level optimization process. GSO consists of inner-level simulations that serve as experimental platforms to evaluate current solutions and provide observational feedback. Outer-level LLMs act as knowledgeable scientists, generating new hypotheses and refining solutions based on this feedback.
It consists of three main components:
- Inner-Level Optimization: Uses simulators to evaluate the current solution and generate observational feedback.
- Outer-Level Optimization: LLMs generate hypotheses based on feedback and refine solutions iteratively.
- Bi-Level Interaction via Model Editing: Adjusts LLM knowledge dynamically using real-time feedback from simulations, mitigating prompt sensitivity issues.
The paper demonstrates GSO’s effectiveness across seven tasks using six different LLM backbones, including Llama3 8B and Mistral 7B.
GSO has been extensively tested on various scientific challenging optimization tasks, including linear system regression, the traveling salesman problem, constitutive law prediction, and molecule property prediction.
Empirical results confirm that GSO significantly enhances optimization performance compared to existing approaches for open and closed source models demonstrating its effectiveness and generalizability.
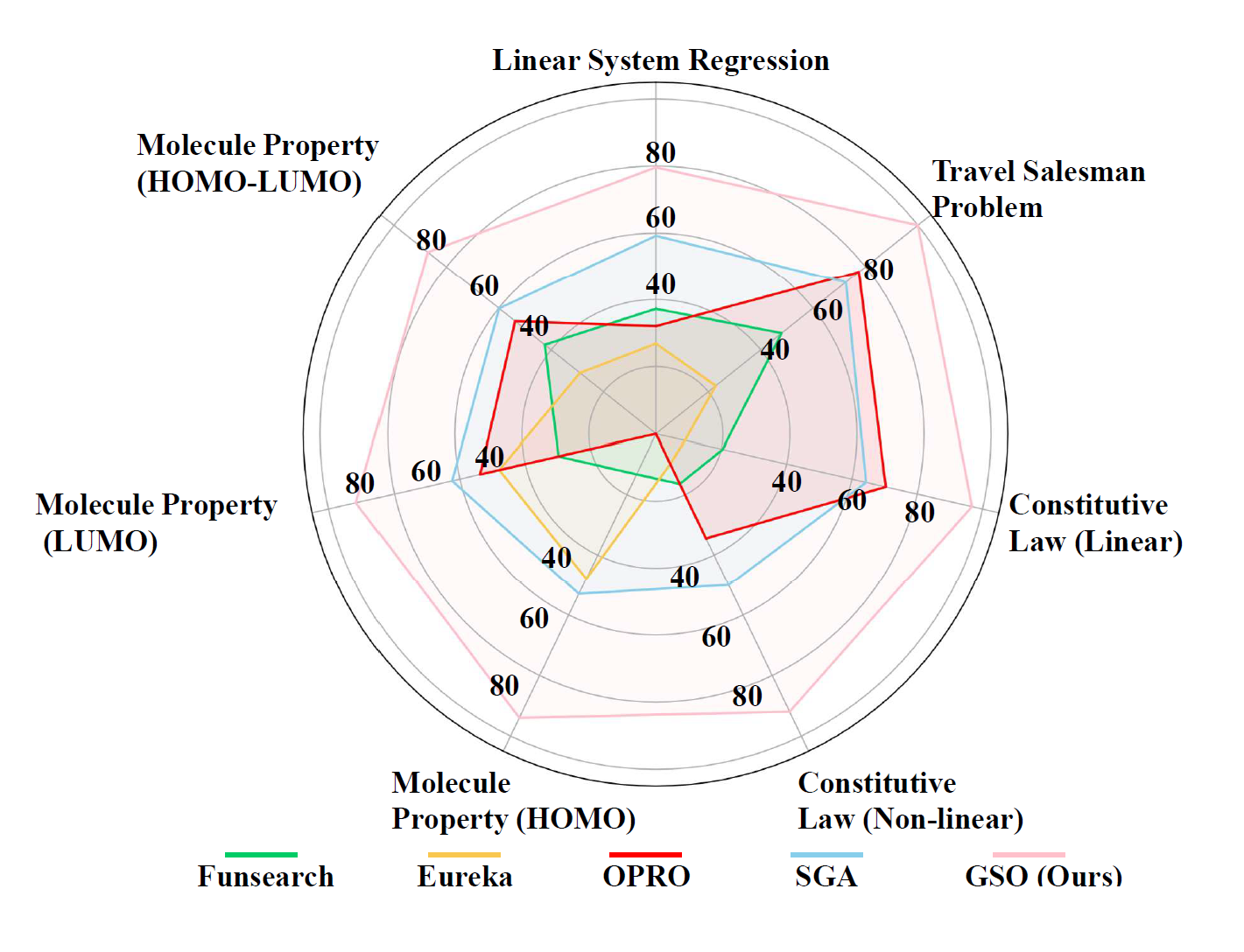
Figure 1: GSO achieves state-of-the-art performance on a broad range of scientific optimization tasks compared with existing methods, using LLama 3 8B (Team, 2024b) as the backbone.
Why It’s Important
The GSO method represents a significant advancement in the field of scientific optimization. By effectively utilizing observational feedback and adapting the optimization direction, GSO can improve the efficiency and accuracy of optimization processes in various scientific domains.
This method has the potential to be applied to other fields beyond scientific optimization, such as engineering, finance, and healthcare, where optimization problems are prevalent.
Additionally, the robustness of GSO to prompt variations makes it a practical tool for real-world applications, reducing the need for extensive prompt tuning. This feature is particularly important in scenarios where the optimization process needs to be adaptable to changing conditions or new data.
- Cross-Domain Applicability: Unlike domain-specific optimization techniques, GSO provides a standardized approach adaptable across multiple scientific disciplines.
- Mitigates Prompt Engineering Challenges: GSO reduces reliance on manually crafted prompts, making LLM-based optimization more accessible and scalable.
- Potential for Future AI-Augmented Science: The integration of model editing into optimization workflows represents a step toward more autonomous, self-improving AI-driven scientific research.
LLMs for Scientific Optimization
Recent research has focused on enhancing LLM performance by incorporating natural language feedback to refine outputs and improve reasoning. These approaches have been applied in various domains:
Reasoning Enhancement: Studies such as Shinn et al. (2023) and Madaan et al. (2024) have explored the integration of iterative self-feedback mechanisms to improve logical reasoning in LLMs.
Code Generation: Methods like those from Chen et al. (2023a) and Olausson et al. (2023) use LLMs to generate and debug code efficiently, leveraging prompt-based refinements.
Dialogue Applications: LLMs have been used to optimize natural conversations and enhance interactive applications (Nair et al., 2023; Yuan et al., 2024; Liu et al., 2024c).
Optimization via External Tools: Techniques such as those proposed by Sumers et al. integrate external computational tools with LLMs to solve complex problems more effectively.
Geometry and Scientific Discovery: The AlphaGeometry model (Trinh et al., 2024) demonstrated LLM capabilities in solving advanced geometric problems without human intervention.
Comparative Optimization Models: Several approaches similar to GSO have emerged:
OPRO (Yang et al., 2023): Uses LLMs as black-box optimizers for reasoning tasks.
Eureka (Ma et al., 2023c): Generates multiple solutions in each step to maximize the success rate of optimization.
Funsearch (Romera-Paredes et al., 2024b): Applies evolutionary strategies to avoid local optima.
SGA (Ma et al., 2024c): Introduces a bi-level optimization model integrating simulations for knowledge refinement.
These advancements illustrate how LLMs are evolving to tackle increasingly complex optimization and scientific challenges.
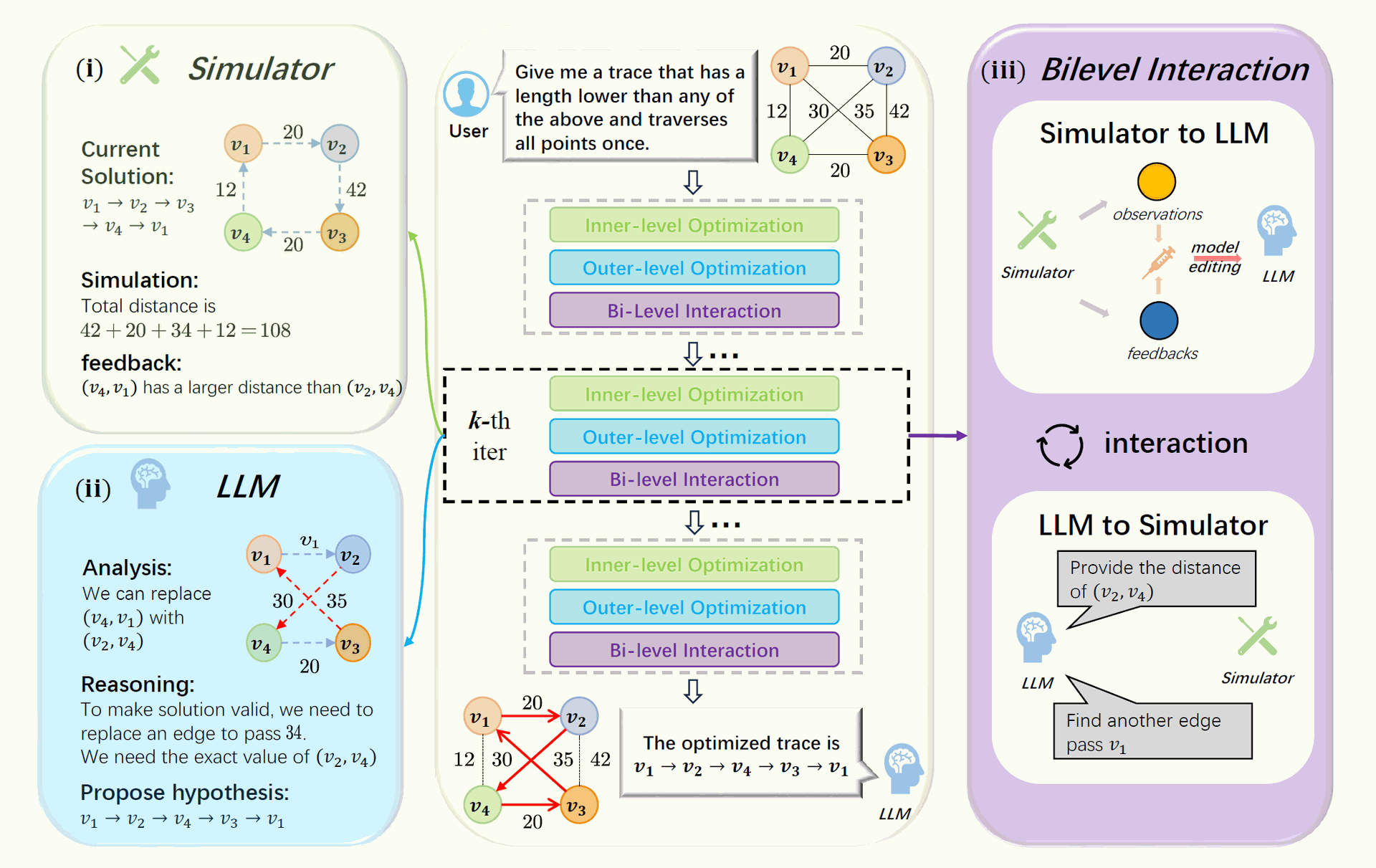
Figure 2: The overview of GSO. For a given optimization task, GSO iteratively conducts the inner-level optimization,outer-level optimization, and bi-level interaction sequentially. The workflow is as follows: (i) the inner-level simulator Φ conducts numerical simulations based on the current step’s hypothetical solution sk (v1 → v2 →v3 → v4 → v1) and returns observational feedback fk,Lk (the edge (v4, v1) has a larger distance than the edge (v2, v4), current total distance: 108); (ii) the outer-level LLM Mθk generates new hypothetical solutions sk+1 (v1 → v2 → v4 → v3 → v1) based on the observational feedback fk,Lk; (iii) the bi-level interaction jointly updates simulations in conjunction with the expert knowledge within the LLMs through model editing.
Process of GSO
The General Scientific Optimizer (GSO) follows a structured iterative process to refine solutions efficiently. As illustrated in Figure 2, the process consists of three key phases:
- Inner-Level Optimization (Simulation-Based Evaluation):
- A simulator serves as an experimental platform, assessing a given solution’s performance.
- Observational feedback is generated, providing insights into performance metrics such as accuracy, efficiency, or errors in the current iteration.
- Outer-Level Optimization (LLM-Based Refinement):
- The LLM analyzes the observational feedback and refines the current solution.
- It hypothesizes new solutions by integrating prior knowledge and iterative learning.
- A dynamic exploit-and-explore strategy adjusts the LLM’s reasoning trajectory based on the received feedback, balancing innovation and optimization.
- Bi-Level Interaction via Model Editing:
- Model editing updates the LLM’s internal knowledge to incorporate insights gained from simulations.
- This process ensures that LLM reasoning aligns with the evolving optimization landscape, preventing the loss-in-the-middle issue caused by long and complex prompts.
- The updated model then provides refined solutions, iterating the process until optimal results are achieved.
By structuring optimization in this bi-level manner, GSO effectively refines solutions while mitigating the limitations of existing prompt-based approaches. The integration of model editing further enhances the adaptability and robustness of LLMs in scientific optimization.
The GSO method was evaluated on a diverse set of scientific optimization tasks to demonstrate its effectiveness and versatility. Here is a detailed description of each problem:
1. Linear System Regression (LSR):
Objective: Estimate the linear coefficients that best model the relationship between input variables and their corresponding responses.
Method: Utilizes a dataset of input-output pairs to find the optimal linear coefficients that minimize the prediction error.
Metric: Number of optimization steps required to find the optimal solution.2. Traveling Salesman Problem (TSP):
Objective: Find the shortest possible route that visits a set of nodes exactly once and returns to the starting point.
Method: Employs a dataset of node coordinates and uses optimization algorithms to find the shortest route.
Metric: Optimality gap, which is the difference between the solution's distance and the oracle solution's distance, normalized by the oracle solution's distance.3. Constitutive Law Prediction:
Objective: Predict the constitutive laws that describe the behavior of materials under stress and strain.
Method: Utilizes a dataset of material properties and stress-strain responses to predict the constitutive laws.
Metric: Mean Squared Error (MSE) between the predicted and actual constitutive laws.4. Molecule Property Prediction:
Objective: Predict molecular properties such as the Highest Occupied Molecular Orbital (HOMO), Lowest Unoccupied Molecular Orbital (LUMO), and the HOMO-LUMO gap.
Method: Uses a dataset of molecular descriptors to predict the molecular properties.
Metric: Mean Squared Error (MSE) between the predicted and actual molecular properties.
These tasks were chosen to cover a wide range of scientific domains and optimization challenges, demonstrating the generalizability and effectiveness of the GSO method.
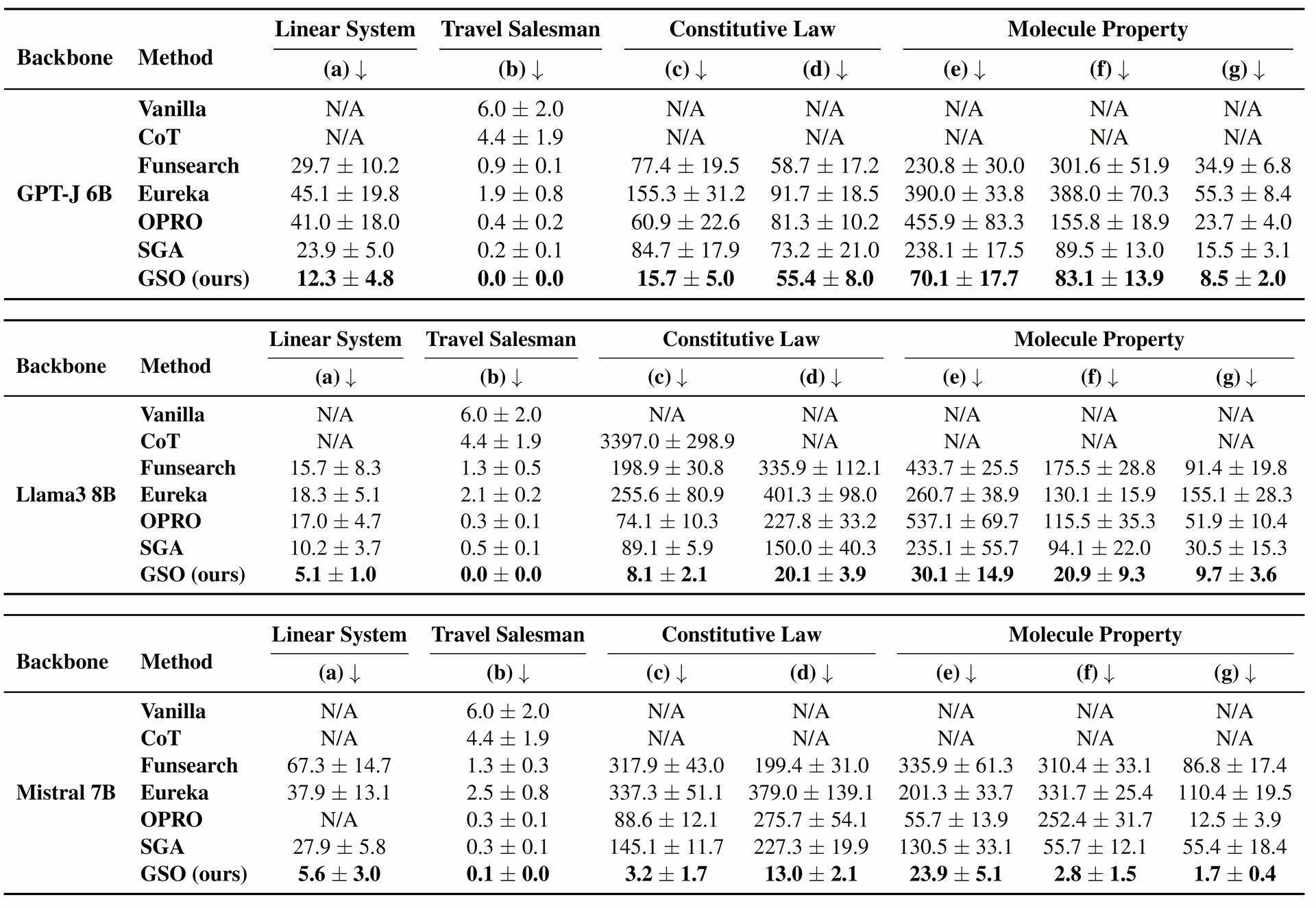
Table 1: Results of our GSO against 6 baselines using GPT-J 6B, Llama3 8B, and Mistral 7B as three representative backbone models (for more results of different backbone models, please see Appendix E). Our experiments encompass 7 different tasks, which are divided into linear system regression (LSR) (a), travel salesman problem (TSP) (b), constitutive law prediction (c-d), and molecule property prediction (e-g). We report the mean ± standard error of each optimization result. The symbol N/A indicates that the model cannot provide a feasible solution for the current task. A lower value is preferable across all tasks. The best results are highlighted in bold text.
Summary of Results
The authors conducted extensive experiments to evaluate the performance of GSO across seven different scientific optimization tasks using six different LLM backbones. The results consistently showed that GSO outperformed existing state-of-the-art methods.
For example, in the molecule property prediction task, GSO achieved a maximum precision improvement of over 32.6 times when utilizing the Mistral 7B backbone model.
It is worth noting there is no mention as to the time complexity of the input for problems such as the traveling salesman. TSP is an NP Hard problem which has an exponential time complexity, meaning it becomes impossible with modern computing to solve as the input (the number of nodes) increases. It can be inferred that the additional time for model editing and computational overhead for GSO will not provide a suitable solution for larger inputs.
The ablation study further demonstrated the importance of each component within GSO. The absence of model editing led to a more significant decline in performance, highlighting the crucial role of effectively utilizing observational feedback to adaptively adjust the optimization direction.
- Superior Performance: GSO consistently outperforms baseline methods in optimization tasks, achieving lower error rates and higher efficiency.
- Ablation Study: Removing model editing or dynamic strategies significantly degrades GSO's performance, proving their importance.
- Robustness to Prompt Sensitivity: Unlike existing prompt-based methods, GSO achieves stable results across different prompt formats.
- Comparison with Closed-Source Models: GSO using Mistral 7B outperforms state-of-the-art models like GPT-4o and Claude-3.5 on optimization tasks.
Conclusion
The paper presents GSO, a novel bi-level optimization framework that integrates LLMs and simulators via model editing. By leveraging structured feedback and iterative refinements, GSO overcomes key limitations of prompt-based optimization methods. The proposed approach demonstrates broad applicability and consistent superiority over existing methods, marking a significant advancement in AI-driven scientific optimization.
References
(Selected references from the paper for citation integrity)
- Amari, S. (1993). Backpropagation and stochastic gradient descent method. Neurocomputing.
- Intriligator, M. (2002). Mathematical optimization and economic theory. SIAM.
- Wang et al. (2023). Scientific optimization with AI. Nature AI.

Exploiting Edited Large Language Models as General Scientific Optimizers